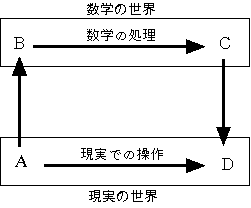
A: 現実についての情報 (1)
B: 数学による翻訳
C: 数学による情報
D: 現実についての情報 (2)
図1
布川 和彦
関心を引き起こす一つの契機として有用性の感得ということがある(大澤, 1996)。例えば、式の変形や公式の適用、論証による新たな定理の確立などは、状況だけに依存した処理では産出の困難な情報を生み出しうる可能性を持ち、Nunokawa (1998)はそこに数学の有用性を求めている(布川, 1998も参照)。大澤(1996)のあげる生徒の感想である、「数学で体育のことなんかできるかと、最初は疑問に思っていたけどバトンパスがうまくいって、タイムもすごく縮んだのですごく驚いた」(p. 251)に見られるように、ここでは有用性がある種の驚きにより感じ取られている。
実際、算数・数学の授業の実践を見ると、驚きや意外性を利用していると思われるものも多い。しかもそこには、大澤(1996)の事例に見られるように、算数・数学と現実とが関わり合っているものがある。そこで本稿では、算数・数学の授業における意外性をある図式にしたがって整理することを試みる。ここで用いる図式とは、問題解決でよく見られる次のようなものである (図1)。

A: 現実についての情報 (1)
B: 数学による翻訳
C: 数学による情報
D: 現実についての情報 (2)
図1
この図式は文章題から立式し、次に計算し、最後にその計算結果を解釈して文章題の答えを求める、という過程を記述するのにしばしば用いられるが、数学的モデル化過程との類似を考慮すると、もう少し広く、数学と現実場面との関わりを考察するための図式として用いたり (Nunokawa, 1998)、式変形などの数学的操作の働きを考察するための図式 (三輪, 1996) としても用いることができる。本稿では、意外性と算数・数学の学習との関わりを統合的に捉えるために、この図式を用いようとするものである(1)。 本稿でこの図式を用いるには、数学の世界と現実の世界を相対的なものとして捉える必要がある。以下では図式中の現実場面は、日常的な場面という意味に限るのではなく、その授業で学ぶことが期待されている算数・数学の知識に対して、より抽象度が低い、あるいは当事者にとって現実性の高い場面を指すことにする。例えば円形の土地の面積を求める際に、これを多角形で近似し三角形の面積の公式を適用することは、数学の処理と考えられる。しかし、円の面積の公式を求める場面で、特定の円に対して多角形で近似し、数値的にアプローチすることは、一般的な公式を正当化するための等積変形などよりは直接的で現実的な方法と考えることにする。
2. A とDとのギャップによる意外性
井上 (1993) は、学ぶ側に「知的好奇心や内発的動機づけ」を呼び起こす授業をめざし、中学校2年生の幾何を中心とした29時間からなる授業を実践している。その最後の4時間では、「大きな課題学習」として、はとめ返しについて考える授業が行われている。1時間目ではまず、長方形のできるはとめ返しを提示し、どうして長方形ができるのかを考え、次に平行四辺形になるはとめ返しを作る。1時間目の最後から2時間目は平行四辺形の課題についての考え方の発表と討論、3および4時間目ははとめ返しでいろいろな図形を作る活動となっている。
ここで、工作用紙で作られたはとめ返しを操作することは、そのしくみを幾何の知識や論証をもとに考えることよりも、生徒にとってより現実的であると考えると、前者が現実の世界の中での流れであり、後者が数学の世界での流れであると考えることができる。井上(1993)によれば、1時間目の最初にはとめ返しの操作を演示したところ、生徒から「あっ、長方形だ」、「どうして長方形ができるんだろう」という声があがったとされている (p. 115)。これは、本稿での図式におけるAとDの間にギャップがあり、そのことが意外性を生み出したものと解釈される。切り口に沿って各部分を裏返すという単純な操作により、 (それほど整っていない) ある図形が別の、しかもかなり整った図形に変形されるという部分で意外性が生じていると考えられる。 どうして長方形ができるのかを考える部分は、数学の世界で図形の性質を用いて考察することで、この意外性のしくみを明らかにすることにあたる。図式でいえば、AからBおよびCを経てDに至る道を確保することで、AとDのギャップを埋めている(図1)。平行四辺形やいろいろな図形を作る活動は、BからCという数学での流れに基づいて、より現実的な世界(工作用紙で作られるはとめ返し)で起こることを予測するものである。
このように見てくると、井上(1993)の実践は最初にA→Dの流れをA→B→C→Dという流れで説明し、次にはA→B→C→Dという流れでA→Dをコントロールしていることになる。AとDのギャップによる意外性を動機づけとするとともに、図1の図式のすべての流れを覆うような形で授業が進められていることが分かる。
フィボナッチ数列による教材(古藤, 1988)を用いた授業も、同様の図式で解釈することができる。この教材では、最初に選ばれた二つの一桁の数に対して一定の簡単な計算をくり返した場合、17番目の結果が第一の数には依存せず、第二の数のみに依存して決まるようになっている。そのため、第二の数を揃えると、17番目の結果は第一の数が異なっていても同じになるという、意外性のある結果が出る。この事例では全ての場合について成り立つことは、手間を惜しまなければ、最初の二数の全ての組み合わせである81通りを調べることで確認はできる。しかし一方で文字式を用いてこの問題を考えること(板垣, 1998)は、場面の仕組みを解明することを可能にすると考えられる。すなわち、最初の2数を x, y としたときに、一連の操作の中でそれら2数がどのように働き、特定の個所ではどのような形で全体の数の中に現れてくるのかを、文字式を使うことで考察することができる。ここでの式による証明は、これら初期値の2数の様子を探るものと考えられ、本当に成り立つのかというよりも、Hanna (1996) の「説明する証明」に当たるものといえる(Hersh (1997)のpp. 59-61も参照)。
ここで実際の数による計算は文字式よりも生徒にとってより現実的であると考えるならば、最初の数の現象としての意外性は、ここでの図式のAとDとのギャップとして捉えることができ、また文字式によりその仕組みを考察することはA→B→C→Dの流れに沿うことを意味する。すなわち、この事例においても図1で表されるような授業の進め方を認めることができる。なお、板垣(1998)の場合には文字による説明に重点が置かれているが、今の図式、あるいは先のはとめ返しの実践との類推で考えるならば、文字式の利用により明らかにされた仕組みに基づいて、現実の世界で生ずることを予測し、それを調べるといった活動を取り入れることも可能であろう。たとえば、計算したときの17番目の結果が、最初に選ばれる第二の数の7倍により決まる、18番目の結果は第一の数と第二の数の和の7の倍数により決まる、などのことが見い出されるが、それらを数の計算のレベルで確かめることが、はとめ返しでいろいろな図形を作る活動に対応するであろう。
屋敷 (1995) は、中学生の確率の授業の際に、生徒達のじゃんけんの記録を集めている。そして、生徒のなかで、チョキとパーを出す割り合いの高い生徒と、チョキを出す割り合いの高い生徒を選び出し、後者の生徒が負けることがあまりないと予測してみせた上で、実際に二人に10回ほどじゃんけんを実行させている。その後、二人のじゃんけんの記録を提示し、確率の考えにより結果を予測できたことを生徒が理解できるようにすることで、「確率の考え方が生活に利用できること」を生徒に伝えようとしている。実際のじゃんけんをし、その結果を調べることを現実での操作と考えるならば、その中で非常に特異な結果が生じており、AとDの間にギャップがあることになる。これに対し、選ばれた二人の行動を確率という言葉に翻訳し、確率の考え方から両者の勝敗を予測することは、数学の処理を経由した流れ、つまりB、Cを経由してDに至る流れとして捉えることができよう。そして、AとDの間にあるギャップが生徒の関心を引き起こし、その後に数学の処理を用いながら現実の世界でのギャップを説明してみせており、この点において、はとめ返しの実践と類似の構造を持つ。 屋敷(1995)でも、A→B→C→Dの流れを利用して現実の世界での事柄を予測するという活動については報告されていない。しかし、例えば、他のクラスなどのデータを生徒たちが自分で集め、それを確率の考えで考察することで、実際のじゃんけんで起こりそうなことを予測し、それを確かめることは、こうした活動に当たるであろう。
3. CとDとのギャップによる意外性
松宮と柳本(1995)は、地元の高層ビルおよび富士山の上から見渡せる範囲を求めるという、中学校数学の授業を報告している。これは、三つの課題からなる「高層ビルの数学」の二番目の課題として計画されているが、彼らによると、三つの課題の中でも生徒たちがもっとも興味を感じた課題とされている(p. 81)。授業は2時間からなり、1時間目では導入の後、見渡せる距離を求める公式を作っている。ここでは、円の接線と三平方の定理を用いて計算することになる。そして、地元の高層ビルおよび富士山から見える距離を求める。2時間目は、2地点からの見える範囲に重なりがあれば、この2地点が互いに見えることが扱われ、最後に見える範囲を地図に記入したものを使い、カレンダーを作成している。
この授業に対する生徒の感想としては、「でけへんと思っていたのができたのでびっくりした」というように、本稿の図式でのAとBとのギャップを示すものも見られるが、同時に数学による処理に基づく結果と、それ以前に自分の持っていた期待とのギャップを示すものも多く見られる(p. 81)。たとえば、「まさか、ツイン21の上からあんなにたくさんの街が見えるとは思わなかった」、「あんな遠くまで見渡せるとは知らなかった」、「僕が思っていたよりも遠くまで見渡せると知ったので、とてもおどろきました」などである。自分のあらかじめ持っていた期待は、数学の処理によらない現実の中での期待と考えるならば、ここでの驚きは図式CとDとのギャップによるものと考えることができる。なお、生徒の感想の中に、「実際にその場所に行って、それがどのくらい正確かやってみたい」というものがあり、数学の処理をした後に、改めてA→Dの流れを意図的に行うことの必要性も示唆されている(2)。また先の感想に見られるように、今の事例では、数学からの情報により現実での期待の見直しが促されている。
坪田(1996)のあげる分数の割り算の事例(pp. 106-115)は、やはり数学の処理と現実における期待とのギャップを利用しながら、しかし両者の役割が異なっている。教師はまず、「 mのひもを
mのひもを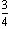 mずつに切ると、ひもは何本できるでしょう」という課題を出すが、これを生徒はすぐに解く。次に、この課題の中の「
mずつに切ると、ひもは何本できるでしょう」という課題を出すが、これを生徒はすぐに解く。次に、この課題の中の「 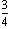 m」の部分を「
m」の部分を「 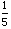 m」に変えるが、生徒は計算をはじめてしばらくすると「おかしい」と感じたと報告されている。そして「おかしい」と感じた理由を話し合っていく中で、計算結果の「
m」に変えるが、生徒は計算をはじめてしばらくすると「おかしい」と感じたと報告されている。そして「おかしい」と感じた理由を話し合っていく中で、計算結果の「 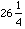 」の が長さではなく割り合いであることが明らかにされ、それを明確にするために教師が図で考え方を示している。
」の が長さではなく割り合いであることが明らかにされ、それを明確にするために教師が図で考え方を示している。
この事例では、AからBの流れはスムーズに行われており、また教師は分かりやすい課題を先に出すことで、あえてこの部分に疑問が生じないように工夫している。また分数の除法の計算も問題なくできるとされている。一方で、長いひもから短いひもをいくつかとるというのは、典型的な包含除の場面であり、何本とれるかはともかく、おおよそどのようになるか、また最後はn本と整数値になること、あまるとすればそれは除数より短くなることなどの期待を、生徒は抱いていたと思われる。したがって、ここでのギャップはこうした現実の世界での期待と計算で得られた結果との間にあったことになる。この部分に「思いもよらない事態」(p. 108)の発生を教師は期待している。このギャップにより開始された話し合いをとおして、「計算の意味」を理解することが、この授業の目標とされている。
一旦生じたギャップは、最終的には教師による図を通して解消されているが、この図は 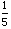 mのひもを1本ずつつないだような図になっている。ここで坪田(1996)は「完成図を作っていく過程を見せる」(p. 113)ことの重要性にふれている。これは、現実での操作("とる" と "つなぐ" の違いはあるが)を図の上で行っていることになる。つまり、CとDとのギャップをA→Dの部分をより明示的にすることによって埋めようとしていると考えることができる。
mのひもを1本ずつつないだような図になっている。ここで坪田(1996)は「完成図を作っていく過程を見せる」(p. 113)ことの重要性にふれている。これは、現実での操作("とる" と "つなぐ" の違いはあるが)を図の上で行っていることになる。つまり、CとDとのギャップをA→Dの部分をより明示的にすることによって埋めようとしていると考えることができる。
4. AとBとのギャップによる意外性
松下(1991)は、等差数列の和の公式を用いてトイレットペーパーの巻き数を求めるという実践(勝野ほか, 1991)を、図1と同様の図式をもとにして分析している。授業は中学生と高校生混成のクラスに対して行われた。この授業では、長さ65mのトイレットペーパーの巻き数を求めるという課題が示された後、勘による予想、全体の半径と芯の半径を知った上での予想、50回ほどいてみせた後の予想をたてさせる。次に等差数列の和の公式を導入し、それを使って巻き数を計算する。その後、実際にトイレットペーパーを全部ほどいて巻き数を数える。最後に、巻き数だけ示された紙テープを各グループに配り、全長を求めるという作業をする、という流れになっている。松下(1991)はこの授業の特徴として、「数学の知識を使うことで現実世界の問題がより効率的に解決できることを実感できるように仕組まれている」(p. 71)ことをあげているが、このことは生徒の感想にも現れている(勝野ほか, 1991, pp. 30-33)。例えば「周りのどんなものでも数学にたとえて計算できることを知りました」「台形の面積を使ってでるなんて、不思議な感じがして、おもしろかったです」「こんな身近なところで、数学が役に立つなんて、すごいと思った」といった感想が見られる。さらに、この授業では最初に現実の場面とそこで求めたいものが示され、次に等差数列の和の公式が導入されているが、この公式が問題解決にどのようにかかわるのかは、導入の時点でははっきりしていなかったとされている。これらより、現実場面で巻き数を求めたいという状態Aと、それを数学的知識により翻訳したものBとの間は、最初から自然に結びついていたものではなく、ここにギャップのあったことがわかる。
この授業ではしかし、後半にギャップが埋められる努力がなされている。すなわち、数学の処理による予測を、トイレットペーパーをほどきながら巻き数を数えるという実験によって確かめているのである。なお、この実験の結果が予測値と合っていたことで、生徒からは歓声と拍手が起きているし、生徒の感想にも「トイレットペーパーの巻き数が、計算した数と合ったときうれしかった」「実験で、計算どおりになってすごいなあと思いました」といった意見がみえる。公式の適用にあたっては、等差数列の和の公式が台形の面積の公式に似ていることにも教師が言及し、さらにトイレットペーパーを実際に切り開いたものを提示して、公式を適用することの妥当性が示されている。しかしこれらの生徒の感想や実験時の拍手は、現実の世界との合致ということが、AとBのギャップを埋める上で重要な役割を果たしていたことを示唆している。この実験は松下(1991)の述べるように、「新しい知識の有効性」(p. 70)を生徒に感じさせるものとなるであろうが、先の図式に沿って考えるならば、数学による翻訳が正当化されたことを意味するであろう。このことは、上であげた生徒の感想からもうかがうことができる。AからB, Cを経由して得られたDと、Aから現実での操作により得られたDとが一致することで、AからBへの移行が生徒に受容されたと見ることができる(3)。
この授業ではさらに、巻き数だけから全長を求め、これを実測値と比較するという活動が行われているが、これも、BとCを経由して長さを予測することと、Aから現実での操作を経て求めたDとの一致により、AからBへの移行の妥当性を確認していく作業と見ることができる。つまり、この授業においても、はとめ返しの授業とはそれぞれの役割は異なるものの、A→B→C→Dの流れとA→Dの流れが相俟って授業が構成されていることがわかる。
柏原(1993)は西瀬戸自動車道の地図を生徒に示し、その全長を求めるという実践を行っている。そこではまず、道路を直線と円弧に分解した上で地図上での長さを求め、次に地図の縮尺から実際の全長を求めている。それらが求まった後で、教師が公団で調べたときの話を生徒にしている。この事例の場合、現実の道路を直線と円弧によりモデル化し、円弧の長さを計算することで道路の全長を求める過程は、本稿の図式のA→B→C→Dにあたるのに対し、公団による実際の測定値を示す部分が現実の世界での操作に対応していると考えることができる。
柏原(1993)は、生徒達の感想としては、「数学で習う弧の長さを利用して因島から向島までの距離を測れたので驚いた」、「こんな曲がりくねったカーブとかでも、数学の公式でとけるなんて、すごい」、「こういった曲線を含んだものは計算できないと思っていたけど、今まで習ったいろんな計算の公式で、いろいろとけるんだなと思った」などをあげている(p. 109)。これらは、曲がりくねった道路の長さを数学に翻訳できることに意外さを感じていたこと、およびそれが確かに可能であったことを生徒たちが感じとっていることを示している。つまり、この授業においても、最初の段階でAからBへの流れにギャップが感じられ、次にA→B→C→DとA→Dとの流れが一致したことで、そのギャップが埋められたものとみることができる。
大澤 (1996) の事例でも、第1節で引用したように、「数学で体育のことなんかできるかと、最初は疑問に思っていたけどバトンパスがうまくいって、タイムもすごく縮んだのですごく驚いた」(p. 251)という生徒の感想があげられている。つまり、AからBへの移行に当初ギャップがあったと考えられる。大澤(1996)は松宮と柳本(1995)の「バトンパスの問題」を取り上げ、中学校3年生に対して実践している。まず各生徒について走ったときのデータを採り、次に前走者の走りを1次関数で、次走者の走りを2次関数で表し、最適と考えられるマークポイント(前走者がそこまで来たら次走者が走り出す地点)を数学的な処理により求める。最後に、実際にリレーを行い、求めたマークポイントを利用することで、タイムが短縮されるかどうかを確かめている。先の感想から分かるように、実際にタイムが短縮されたことが、数学を応用することの妥当性を支えている。つまり、A→Bのギャップは、A→Dという現実での操作とB, Cを経由して得られた情報との合致により埋められている。
出口(1997)は「コインと統計」という一連の授業を中学校2年生に対して実践している。授業ではまず各硬貨の発行枚数が扱われた後、2時間目からは最も多い1円玉を取り上げ、標本に基づいて、発行枚数が年ごとに違うのかを調べている。最初は各自が持ってきた20枚を用い、次にグループで合わせて100枚、さらにクラス全体(500枚程度)のものでグラフを作り、発行枚数に関する予想をしている。その後で、1円玉の実際の発行枚数のグラフを配付し、標本から作られたグラフと比較している。同様の作業を10円玉、100円玉についても行っている。なお、10円玉の作業が終わった時点で、標本調査の考えを知らせ、それがどのような場面で利用できそうかを問い、また授業の最後では発行枚数に差があることを、社会現象(スーパーマーケットの出現、消費税の導入)と結び付けて説明している。
1円玉の作業が終わった時点での生徒の感想を見ると、「500枚ぐらいでだいたいの枚数がわかるのはすごい」、「何億枚というのと500枚くらいというのでは差がありすぎてしらべられないと思っていたのに、表と自分たちのとをあわせてみると、ほとんどかわらなかったのでびっくりしてしまった」(pp. 187-188)というものがある。標本調査という手法を数学の処理と考えるならば、これらの生徒の感想は、AからBへの移行が妥当なのかに関わってギャップが存在したことを示している。そして、実際の発行枚数を知ることを現実での操作と考えるならば、B, Cを経由して得られた情報と、A→Dにより得られる情報とがかなり合致することが、この妥当性を支えている。つまり、A→Dによって先のギャップは埋められている。
5. BとCとのギャップによる意外性
このギャップはいわば、数学の処理に関して、本当にそんなことができるのか、といったギャップと考えられる(註(1)を参照)。池浦(1996)の実践に、こうしたギャップを見い出すことができる。
彼女は小学校5年生の円の面積を求める2時間続きの授業を報告している。教師は知っている図形で面積を求めていない図形が何かを問う中で、「円の面積の公式もだせるかな」と発問している。図形や数値が与えられたときに公式などを利用して面積を求めることを、数学の世界での処理と考える(Nunokawa, 1998)ならば、円の面積がいくつかではなく、その公式が導けるかを問うことは、BからCへの移行が可能かを問うていることになる。さらに他の公式をどのように求めたかを想起させ、円を公式を知っている図形に直せないかと問う。この問いに対する生徒の反応を見ると、「円はできないよ」「曲線だからできないと思う」といったものであり、「ほとんどの子供が円は曲線だから、今までの学習は使えない」と考えたとされる。池浦(1996)は「教師の思っている以上に曲線への抵抗が大きかった」(p. 8)と述べている。ここにおいて、BからCへ向かう部分でのギャップを認めることができる。また円を16個の扇形に分け、組み合わせて平行四辺形のように変形する考え方は、生徒からは出ず、教師のヒントプリントとして導入されているが、この段階においても、曲線の部分を気にする生徒が見える。これもBからCへの移行の途中でのギャップと見ることができよう。この授業では、公式がはっきりした瞬間、拍手が起こったとされるが、これはBからCへのギャップが埋まった時点でもある。
布川(1998)においては、新しい概念や技能の導入においては、図1の図式ではなく、その中のAからBの矢印、およびCからDの矢印を逆向きにした図式が想定されている(p. 106)。しかし、この授業でのギャップの埋め方は単純な迂回、すなわちB→A→D→CとしてCに至るというものではなかった。むしろ数学の世界での処理と現実での操作を行き来している。上でも述べたように、教師はまず公式を知っている図形に直すことを提案するが、これは数学の世界での処理(等積変形)である。しかし教師はすぐに公式に至る変形を導入せずに、話し合いを通して多角形に直しておよその面積を求める方法を明らかにし、半径5cmの円の面積を求めている。第1節で述べたように、円の面積を求めるという文脈からすると、三角形に分割し面積を求めることは、生徒にとってより現実的な課題と考えられる。また多角形の角数を増やすことでより正確になるという考えが出され、360角形の面積を計算する生徒が出てくるが、これは直接的な求積で近似の精度をあげるという意味で、公式を求めることよりもやはり現実的なレベルでの思考と見ることができる。同時にこの段階で、上で述べたように、平行四辺形になおす考えがヒントプリントで導入されるが、こちらはB→Cの流れの一部を導入していることになる。2時間目の最初にはこの変形の仕方を、紙を切って操作することで確かめている。扱われていることは等積変形であり、ここでの数学の処理と言えるが、池浦(1996)は円が実際に他の形になることが「おもしろかったようである」と報告しており、相当する操作を現実の世界でやったことに意味があると考えられる。公式に至る部分は、360角形による考え方の式を変形すると、等積変形による考え方の式と同じものが出てくることに依っているが、それを比較する契機は、両者の面積の価が等しくなったことである。つまり、公式自体は数学の処理を通して確立されたが、それ以前に数値上の一致という、より現実的なレベルでの情報が影響していたことになる。以上のように、この実践でのギャップの埋め方は、現実での操作に支えられながら、数学の処理を少しずつ進める形になっている。
中川(1997)の事例では、BからCのギャップが内発的に生じている。彼は小学校4年生の面積の授業の中で、2cm2 のいろいろな形を考える時間をとっている。ある生徒は、2×1の長方形を1×2に「つぶしていく間に」正方形になるであろうことから、面積2cm2の正方形が「必ずある」(p. 169)と考えている。彼は2cm2の長方形を分割し並べ換えたり、平方して2になる数を計算により求めようとしている。しかしそれらに失敗し、「絶対、見つけ出すつもりだったのにできなかった」と書き残している。そして、話し合いの中で他の生徒が2cm2の正方形を示すと、「思わず身を乗り出して聞いていた」(p. 169)とされる。図形に対する漠然としたイメージをより現実的なものとすれば、今の生徒の例では、A→Dがその存在を保証し、「必ずある」と考えながら、それが数学の操作(等積変形)により実現できないところにギャップが生じていると言える。ギャップの解消は、他の生徒による等積変形の提示によっているが、当該の生徒の試みは等積変形のほかに、数値計算にもよっている。先ほどの円の面積の場合と同様、このやり方をより直接的で現実的なものと考えるならば、この生徒の試みは、やはり現実での操作と数学での処理の双方を含むものであったと言えよう。
なお中川(1997)は、2cm2になるのは長方形だけだと考えた他の生徒についても述べている。この生徒の場合も、他の生徒による等積変形を見たときに「目がさめたような顔つき」になり、その考えを「わざわざノートに書き、『すばらしいと思う』と称賛の言葉を」書いたとされる(p. 169)。この生徒の場合は、埋まらないのではないかと思っていたB→Cが埋まったことに驚きが生じており、円の面積の事例と類似の構造を見ることができる。
6. 事例に見られる共通点
以上の事例に共通する点を考えてみる。
第一に、それぞれの事例では、ギャップが意識されやすいような工夫がなされている。はとめ返しやじゃんけんの例では、現実での単純な操作が意外な結果を生むようになっている。例えば、はとめ返しの操作が複雑なものであったならば、長方形のような整った形になってもそれほど驚きが起こらなかったかもしれない。トイレットペーパー、道路の全長、バトンパスの事例では、ある程度複雑な現象を用いることで、本当に数学が使えるのかという気持ちを高めていると考えられる。と同時に、現実の中で確認する方法はあっても、自分たちで実行するには多少困難を伴うような現象にもなっている。また硬貨の発行枚数の事例では、生徒自身が持ってきた1円玉を使っているが、教師がコントロールしたのではない素材を使うことも、結果の意外性を高めていると考えられる。高層ビルの事例は、生徒が漠然とした期待を持ち、かつそれが実際の現象とずれているような題材が選ばれたと考えられる。分数の除法の事例では、本来の問いの前に、除法で生徒の期待通りの答えが得られる別の問いを置き、その問いに簡単な操作を加えることで本来の問いを引き出している。これにより、ここでのギャップがより意識されることになったであろう。円の面積では、面積を求めてみようではなく、まず公式を作ることができるかどうかを直接問うている。中川(1997)の事例では、あえて平方数ではない面積を扱っている。
意外性の意味から当然のことではあるが、これらのギャップは生徒の側のある種の期待を前提にしている。現実での操作として単純なものを選ぶこと(4)、現象として複雑なものを選ぶこと、生徒自身が準備した素材を用いること、生徒の期待に沿って解決できる問いを先に置くことは、こうした期待を強めるための工夫と見ることができる。大澤(1998)の事例では、2次関数により表される現象を生徒は最初、比例により表現している。生徒の漠然とした期待によりまずモデル化させ、それと現象とのギャップを明らかにすることでモデルの見直しが自主的に生ずるための工夫とこれを見るならば、生徒の側の期待をより明示的に利用した例と言えよう。
第二に、いずれの事例も数学の世界と現実の世界の両者を組み合わせており、特に数学の処理を確立する第5節の事例を除くと、他の事例では図1の流れが全て現れるようになっている。さらに、現実の世界が生徒にとってより納得しやすい世界であることを反映していると思われるが、全般的には現実の操作により数学の処理あるいは数学の適用の妥当性を示す事例が多くなっている。第4節の事例は全てそうであったが、分数の除法でも最後の確認は、現実に近い図によるものであった。はとめ返しの事例でも、数学の処理に基づいて作った新たなはとめ返しを実際に操作することでその処理を確かめることはできよう。高層ビルの事例でも生徒の側には現実により確認をしたいという希望が見られた。つまり、これらの例では、数学の処理を支えるために、当該の数学より具体的な操作も、大切な側面を担っていることになる。
7. おわりに
本稿では、いくつかの授業における意外性や驚きのタイプを、図1のような問題解決の研究などでよく見られる図式により整理してきた。そこで見られたタイプをまとめると、以下のようになる。
また意外性が生徒の期待を前提とすること、本稿で考察した事例の多くでは、現実での情報により数学の処理を妥当化する工夫がされていることに言及した。例えば、既に確立された数学の処理について、改めて現実との適合を示すことを授業の計画の中で考慮することもできるであろう。さらに、意外性が生じ、かつこれが解消されるには、当該の授業内容に関して生徒がどのような期待を持つのか、あるいは生徒はどのような証拠を示せば納得をするのかを考えることも必要になってくるであろう。
註