論文の最初に彼らはまず、問題に関連したどのような知識を持っているかを示す指標と、知識の結びつきの状態を示す指標とを区別する。前者は内容指標(content indicators)、後者は連結性指標(connectedness indicators)と呼ばれる。

　問題解決の研究で多く用いられてきた生徒に書かれた解答の分析や発話思考法、知識の想起などは、内容についての情報は与えるが、知識の組織化の状態を調べるにはもっと他の手続きが必要である。彼らは、単語連想法や概念地図法などの先行研究を概観した後、自分たちの用いる手続きとして以下のようなものをあげている。

• 反応時間・・・図に示された知識要素を認識するのに必要な時間
  
• 体系的なヒント・・・ヒントのレベルを変えて与え、アクセスに必要なヒントのレベルにより知識の活性化の程度をはかることで、一つの知識スキーマ内の要素の結びつきについての情報を得る
  
• 問題作り・・・解決において当該のスキーマを必要とするような問題を作らせる
  
• 精緻化課題・・・当該のスキーマを他のスキーマと直接結びつけさせることで、それらが互いに どのように関連しているかをみる
  

　各生徒は１人ずつ、60分のセッションに２回参加する。第１セッションは４つの、第２セッションは３つの課題からなっている。

第１セッション
(1) 自由想起課題
　知っている幾何学の定理や公式をあげてもらう。効果的に組織化されたスキーマを持っている場合、スキーマ内の知識がより多く検索されると期待されている。想起された定理の数が得点となる。
(2) 問題解決課題
　平面図形についての４つの問題を解いてもらう。援助の内状態での知識の活性化の様子をみる。解決の様子に応じて、０〜２の得点が与えられる。
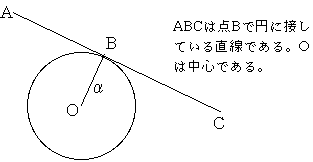
(3) 幾何学的要素課題
　問題に関連した図が示され、どのような部分（かたち）があるか、どのような規則や定理が含まれているかが問われる。例えば、下のような図が示されたとき、それに関わる規則としては「円の接線は接点での半径に直交する」といったものがある。

第２セッション
(1) 認識課題
　コンピュータ・ソフトを用い、スクリーンに図１のような図形が現れたときに、そのある部分をクリックすることでその要素を認識するまでの時間をはかる。クリックした後、その要素の名称をタイプすることになっているが、この論文では正しい認識の反応時間がだけがデータとして使われている。
(2) 応用課題
　５つの定理や公式が示され、それぞれを用いる事例を報告させる。これにより、その定理や公式に関連したスキーマ内の要素間の結びつきをみる。例を示せない場合はヒントとして簡単な問題例を与える。事例の正しさとヒントの有無により得点は０〜５となる。
(3) 精緻化課題
　定理または公式からなるペアを一度に１ペアずつ提示する（例えば、定理１「円の中心から弦に下ろした 垂線はその弦を二等分する」と定理２「ピタゴラスの定理」）。　そして両方の定理を使うような問題を 作らせる。関連するスキーマどうしを結びつけられるかをみる。結びつきに応じ０〜４の得点となる。

　結果は統計的な処理から得られている。まず問題解決課題ではＨＡとＬＡとに有意な差が見られた。内容指標には自由想起課題と幾何学的要素課題が、連結性指標にはヒント課題、応用課題、精緻化課題、認識課題が含まれているが、この両者も有意な差があった。つまり、ＨＡ群は問題に関連したより広範囲の知識に アクセスすることができ、また知識の組織においても優れていたと言える。さらに細かい分析により、内容指標では両群の差に最も貢献していたのは、要素課題の中の規則や定理の認識であった。連結性指標は全体的に内容指標よりも効果のサイズが大きく、連結性指標の中ではヒント課題と精緻化課題での両軍の差が大きい。どちらの群のメンバーかを予測するのにどの指標が最も重要かを調べるため、彼らは判別分析を行っている。この結果からも、内容指標よりも連結性指標の方が強く貢献していることが示唆される、としている。

　最後の節ではまず、それぞれの課題の結果を振り返り、ＨＡ群の生徒ではＬＡ群の生徒よりも知識の 結びつきが豊かであり、これが問題解決の成績に影響を与えていることがまとめられる。成功的な 問題解決は、よく組織されまたより広がりを持った知識ベースにより引き起こされている。なお、 それに関わり、 エキスパートの解決者は幾何学の知識を単一の典型的なイメージに結びつく事実の集まりの形に組織化している、という、KoedingerとAnderson (Cognitive Sience, vol.14) のモデルにも言及しているが、 Lawson氏らは特定のスキーマのフォーマルなモデルを作ることを目的としていないということで、 それ以上は議論していない。ただし、彼らの用いた手続きは解決者の幾何学の「知覚的チャンク」に 迫りうるものと主張し、本論文の結果が、ＨＡ群の知覚的チャンクがより良い質のものであることを 示唆するとしている。

　上記の結果を踏まえてLawson氏らは２つの示唆をあげている。一つは、あるトピックについて生徒が 発展させているスキーマについて、それを提示したり議論したりするような時間を、授業の中で設けるべきということである。解決が得意でない生徒ほどこうした議論が必要となる。二つ目は評価に関わるもの である。本稿で用いられた課題、特に精緻化課題と応用課題は、他の方法では活性化されないかもしれ ない知識の結びつきを要求する。こうした情報を持つことで、教師は生徒の理解状態についてのより 豊かなイメージを持つことでき、生徒の直面する困難に関して判断をすることができる、としている。

　この論文は、知識の結びつきを調べるいくつかの課題を工夫し併用することで、知識の状態が 問題解決に影響を与えることを示している。指導においても評価においても知識の結びつき に注意を向けねばならないとする彼らの示唆も、妥当なものと言えよう。しかし、どのような知識が どのように結びついていたのかといった、連結性の具体的な様相についての議論はなく、したがって、 スキーマの状態が実際の解決活動にどのように影響を与えたのか、についても言及はない。解決活動の 特性をより良く知る上でも、生徒への支援を具体的に行う上でも、こうした点をさらに調べていく 必要があるのではないだろうか。