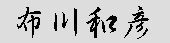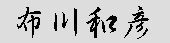Kazuhiko Nunokawa

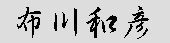
(Mathematics Education)

Martian Version
Meditation Version
Onion Version
Portraits by 3rd-graders of our attached school

I am interested in human's thinking processes in mathematical problem solving, and their relations to the nature of mathematical knowledge. Maybe, the human is a being that cannot help making sense of the world and mathematical knowledge is one of various materials used to do that.

Recent Publications

• Nunokawa, K. (1998). Empirical and autonomical aspects of school mathematics. Tsukuba Journal ofEducational Study in Mathematics, 17, 205-217.(41K)
• Nunokawa, K. (1997). Giving new senses to the existing elements: A characteristic of the solutionaccompanied by global restructuring. Journal of Mathematical Behavior, 16 (4), 365-378.
  
• Nunokawa, K. (1997). Physical models in mathematical problem solving: A case of a tetrahedron problem. International Journal of Mathematical Education in Science andTechnology, 28 (6), 871-882.
  
• Nunokawa, K. (1997). Microanalysis of the ways of using simpler problems in mathematical problem solving.�@Proceedigns of the 21st Conference of the International Group for the Psychology of Mathematics Education (Vol. 3, pp. 296-303). Lahti, Finland.(48K)
  
• Nunokawa, K. (1997). Data versus conjectures in mathematical problem solving. Focus on Learning Problems in Mathematics, 19 (1), 1-19.
  
• Nunokawa, K. (1996). Applying Lakatos' theory to the theory of mathematical problem solving. Educational Studies in Mathematics, 31 (3), 269-293.
  
• Nunokawa, K. (1996). A continuity of solver's structures: Earlier activitiesfacilitating the generation of basic ideas. Tsukuba Journal ofEducational Study in Mathematics, 15, 113-122.
  
• Nunokawa, K. (1995). Problem solving as modelling: A case of augmented-quotientdivision problem. International Journal of Mathematical Education in Science andTechnology, 26 (5), 721-727.
  
• Nunokawa, K. (1994). Solver's structures of a problem situation and their globalrestructuring. Journal of Mathematical Behavior, 13 (3), 275-297.
  
• Nunokawa, K. (1994). Improving diagrams gradually: One approach to using diagramsin problem solving. For the Learning of Mathematics, 14 (1), 34-38.
  
• Nunokawa, K. (1994). Naturally GeneratedElements and Giving Them Senses: A Usage of Diagrams in Problem Solving.In J. P. Ponte & J. F. Matos (Eds.), Proceedings of the 18th International Conferencefor the Psychology of Mathematics Education, vol. III (pp.376-383). Lisbon: Universityof Lisbon.
  
• Nunokawa, K. (1994). Solvers' Spontaneous Balancing of the Level of Difficulty in Mathematical Problem Solving. Tsukuba Journal ofEducational Study in Mathematics, 12 (B), 47-56.
  

In Press

• Nunokawa, K. (in press). Heuristic Strategies and Probing Problem Situations. In Jose Carrillo & Luis C. Contreras (Eds.), Problem-soling in the beginning of the 21st century: An international overview from multiple perspectives and educational levels. Servicio de Publicaciones, Universidad de Huelva.

Department of Mathematics Homepage

Please let me know your impression about this page and imformation about math education:nunokawa@juen.ac.jp