Asymptote 3次元グラフィックス
整数論とTeXに関するページ Last UpDate: 2021/11/08
線分・ベクトル
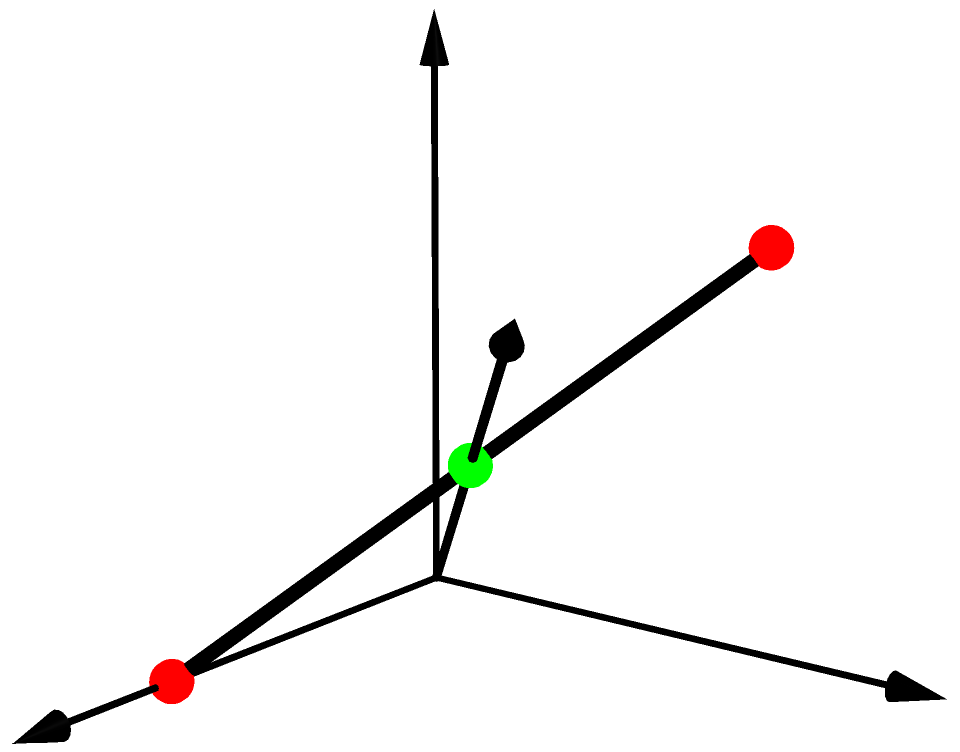
空間における点、線分、ベクトルを描くには次のように書きます。3次元グラフィックスにはimport threeという命令を使います。
settings.outformat = "pdf"; settings.render=16; settings.prc = false; unitsize(1cm); import three; dot((1,0,0),red); dot((0,1,1),red); dot((1/2,1/2,1/2),green); draw((1,0,0)--(0,1,1), linewidth(1pt)); draw((0,0,0)--(1.5,0,0), Arrow3(4)); draw((0,0,0)--(0,1.5,0), Arrow3(4)); draw((0,0,0)--(0,0,1.5), Arrow3(4)); draw((0,0,0)--(1,1,1), linewidth(0.7pt),Arrow3(4));
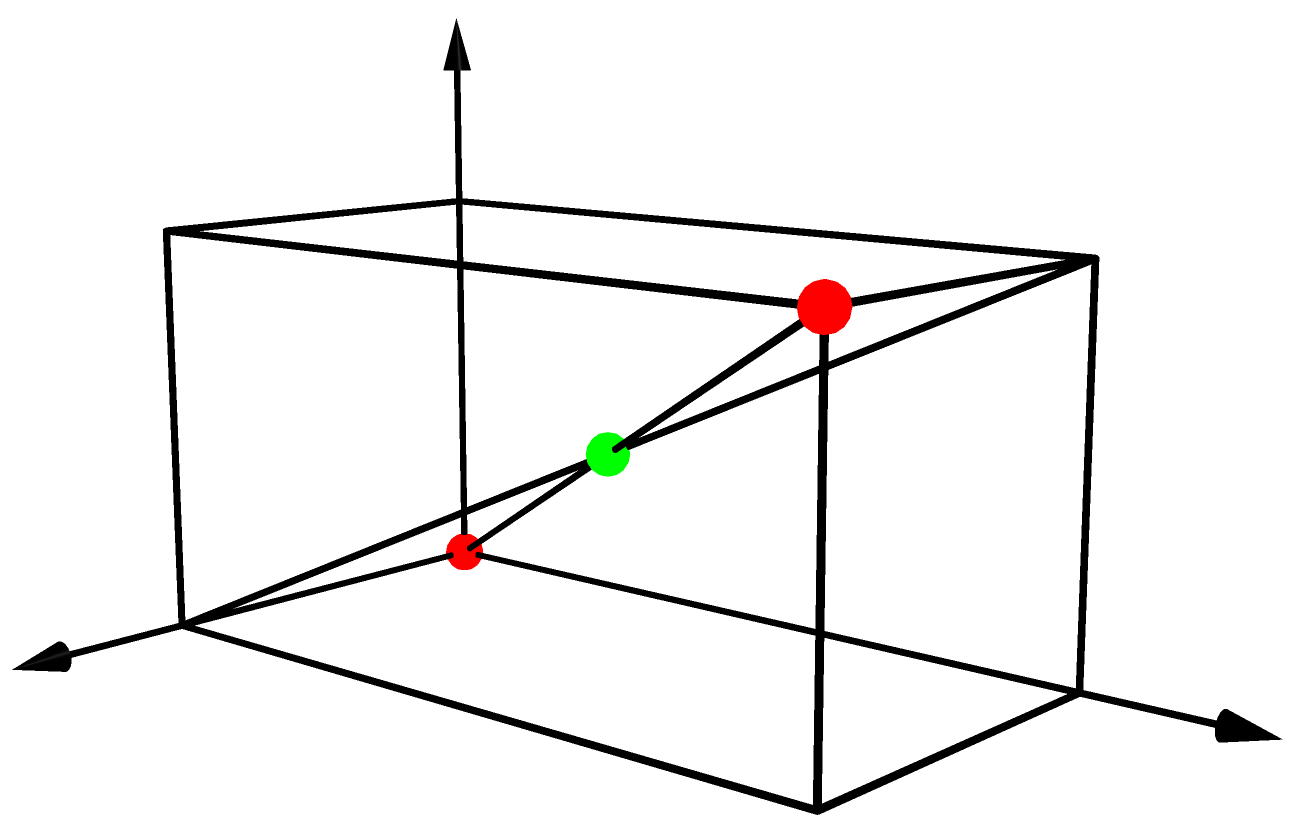
直方体
新規タブで開く
直方体を描くには次のように書きます。perspective(4,4,1.5)は視点の座標を(4,4,1.5)にするという命令です。settings.outformat = "pdf"をsettings.outformat = "html"にして生成されたhtmlファイルをブラウザで見れば自由に図形を回転させることができます。
settings.outformat = "pdf"; unitsize(1cm); settings.render=16; settings.prc = false; import three; currentprojection=perspective(4,4,1.5); dot((0,0,0),red); dot((1,2,1),red); dot((1/2,1,1/2),green); draw((0,0,0)--(1,2,1)); draw((0,0,0)--(1.5,0,0), Arrow3(4)); draw((0,0,0)--(0,2.5,0), Arrow3(4)); draw((0,0,0)--(0,0,1.5), Arrow3(4)); draw((1,0,0)--(0,2,1)); draw(box((0,0,0),(1,2,1)));
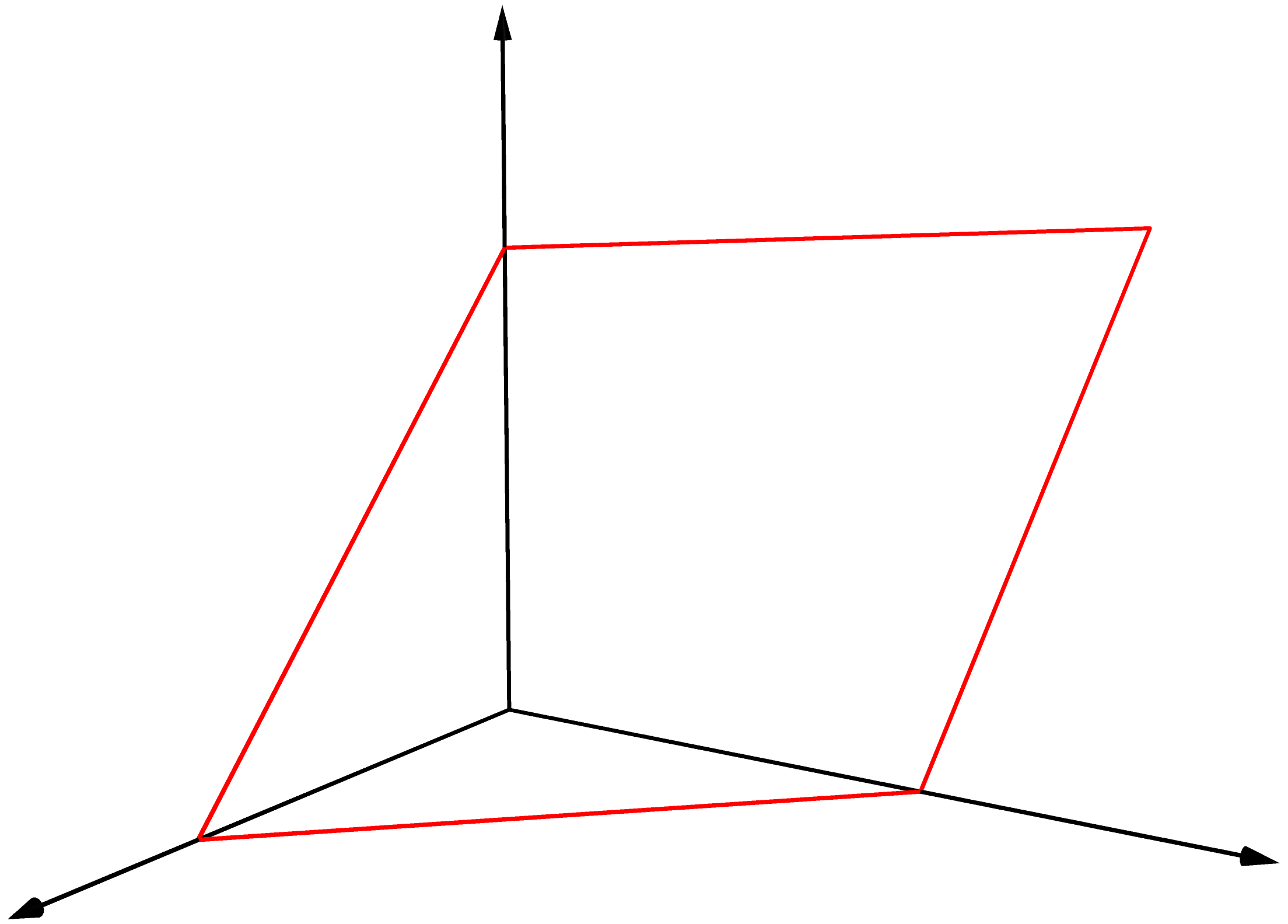
空間における平行四辺形
新規タブで開く
空間における平行四辺形を描くには次のように書きます。plane(v1,v2,p1)は点p1を通り,ベクトルv1とベクトルv2で張られる平行四辺形を与える命令です。
settings.outformat="svg"; settings.render=16; import three; size(2cm,0); draw((0,0,0)--(1.5,0,0), Arrow3(4)); draw((0,0,0)--(0,1.75,0), Arrow3(4)); draw((0,0,0)--(0,0,1.5), Arrow3(4)); draw(plane((-1,1,0),(-1,0,1),(1,0,0)),red);
空間における円・円弧
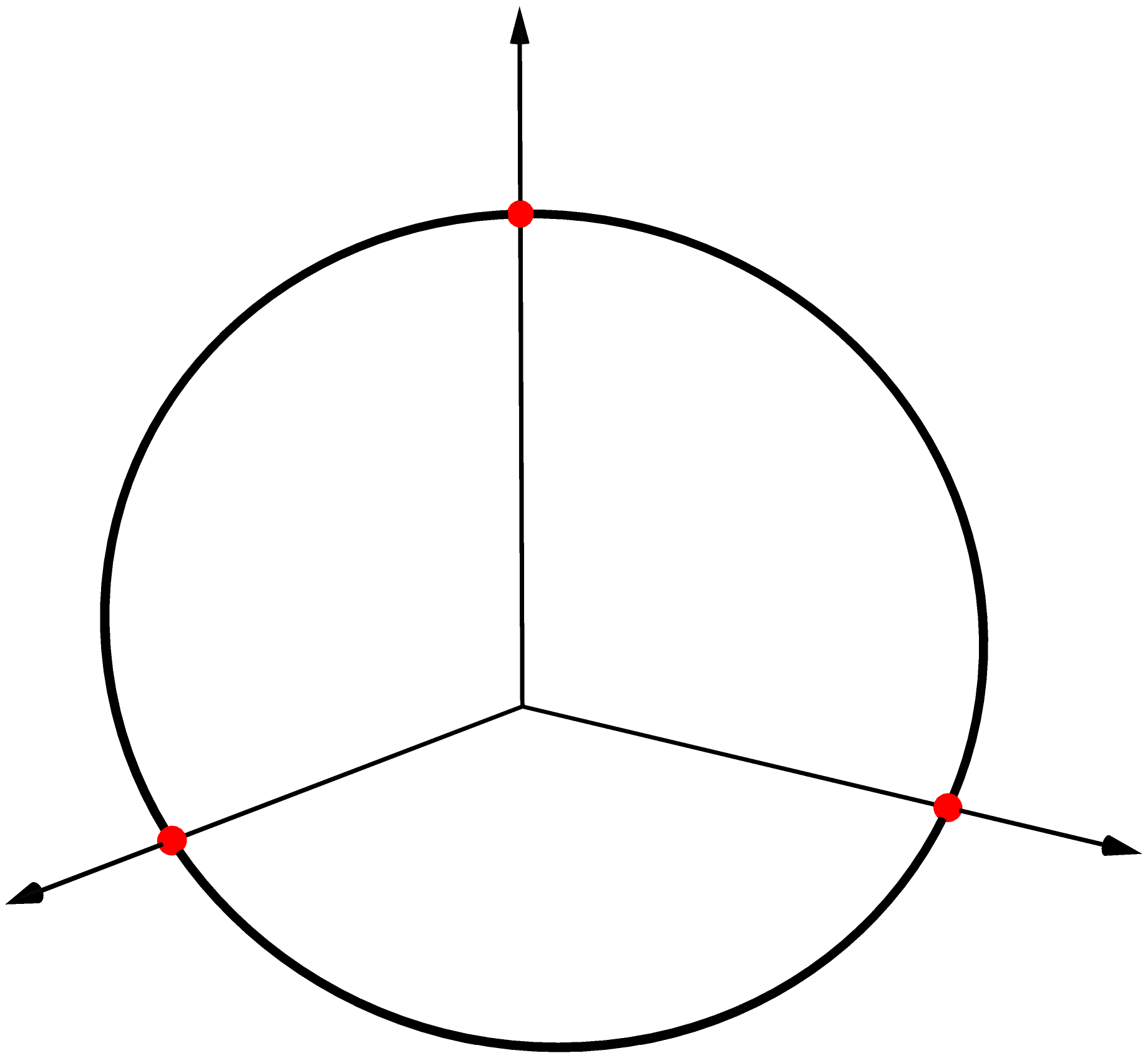
空間における円を描くには次のように書きます。ここでOは(0,0,0)、X、Y、Zはそれぞれ (1,0,0)、(0,1,0)、(0,0,1)を略記して表したものです。X+Y+Zは(1,1,1)を表します。 circle(c,r,X+Y+Z)は、中心がc、半径がrでベクトルX+Y+Zと垂直な円を生成する命令です。
settings.outformat="pdf"; settings.render=16; settings.prc = false; unitsize(2cm); import three; real r=sqrt(6)/3; triple c=(1/3,1/3,1/3); draw(O--1.4X, Arrow3(4)); draw(O--1.4Y, Arrow3(4)); draw(O--1.4Z, Arrow3(4)); draw(circle(c,r,X+Y+Z), linewidth(1pt)); dot(X,red); dot(Y,red); dot(Z,red);
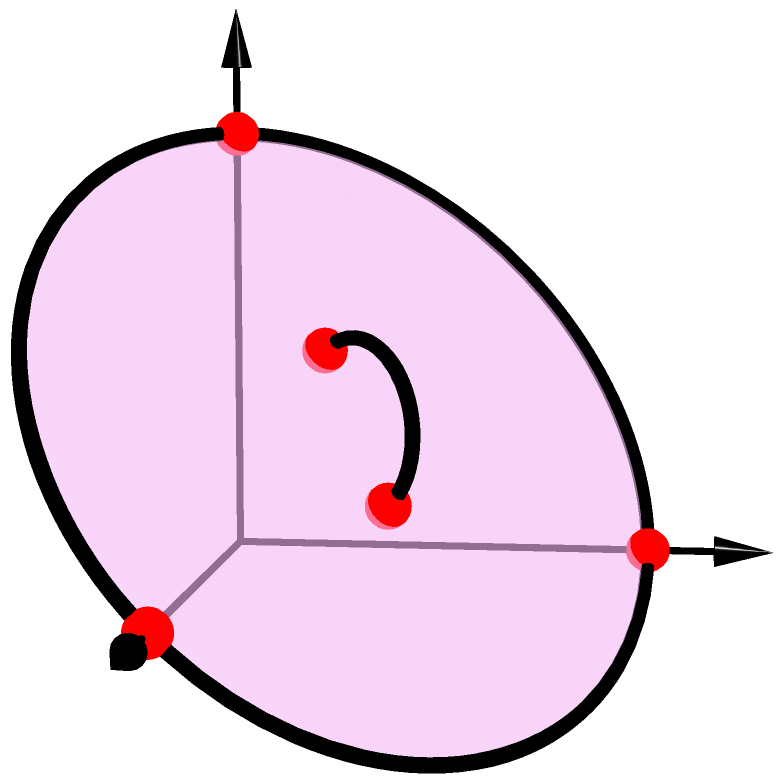
空間における円弧を描くには次のように書きます。arc(c,p1,p2)は 中心がc、p1を始点として、cとp2を結ぶ直線上に終点をもつ円弧を生成する命令です。 デフォルトでは円弧の角度は180度以下です。ただしこの例のように3点c,p1,p2が一直線上にあるときは さらに円弧と垂直なベクトルを指定する必要があります。 例ではY-X=(-1,1,0)を円弧と垂直なベクトルとして指定しています。 3点c,p1,p2が一直線上にないときもこれを指定することによって円弧の角度を180度より大きくすることができます。
settings.outformat="pdf"; settings.render=16; settings.prc = false; unitsize(1cm); import three; currentprojection=perspective((5,1,1)); real r=sqrt(6)/3; triple c=(1/3,1/3,1/3), p1=(1/4,1/4,1/2), p2=(5/12,5/12,1/6); draw(O--1.3X, Arrow3(4)); draw(O--1.3Y, Arrow3(4)); draw(O--1.3Z, Arrow3(4)); path3 C0=circle(c,r,X+Y+Z); surface S0=surface(C0); draw(S0, surfacepen=pink+opacity(0.6)); draw(C0, linewidth(1pt)); draw(arc(c,p1,p2,Y-X), linewidth(1pt)); dot(X,red); dot(Y,red); dot(Z,red); dot(p1,green); dot(p2,green);
空間曲線
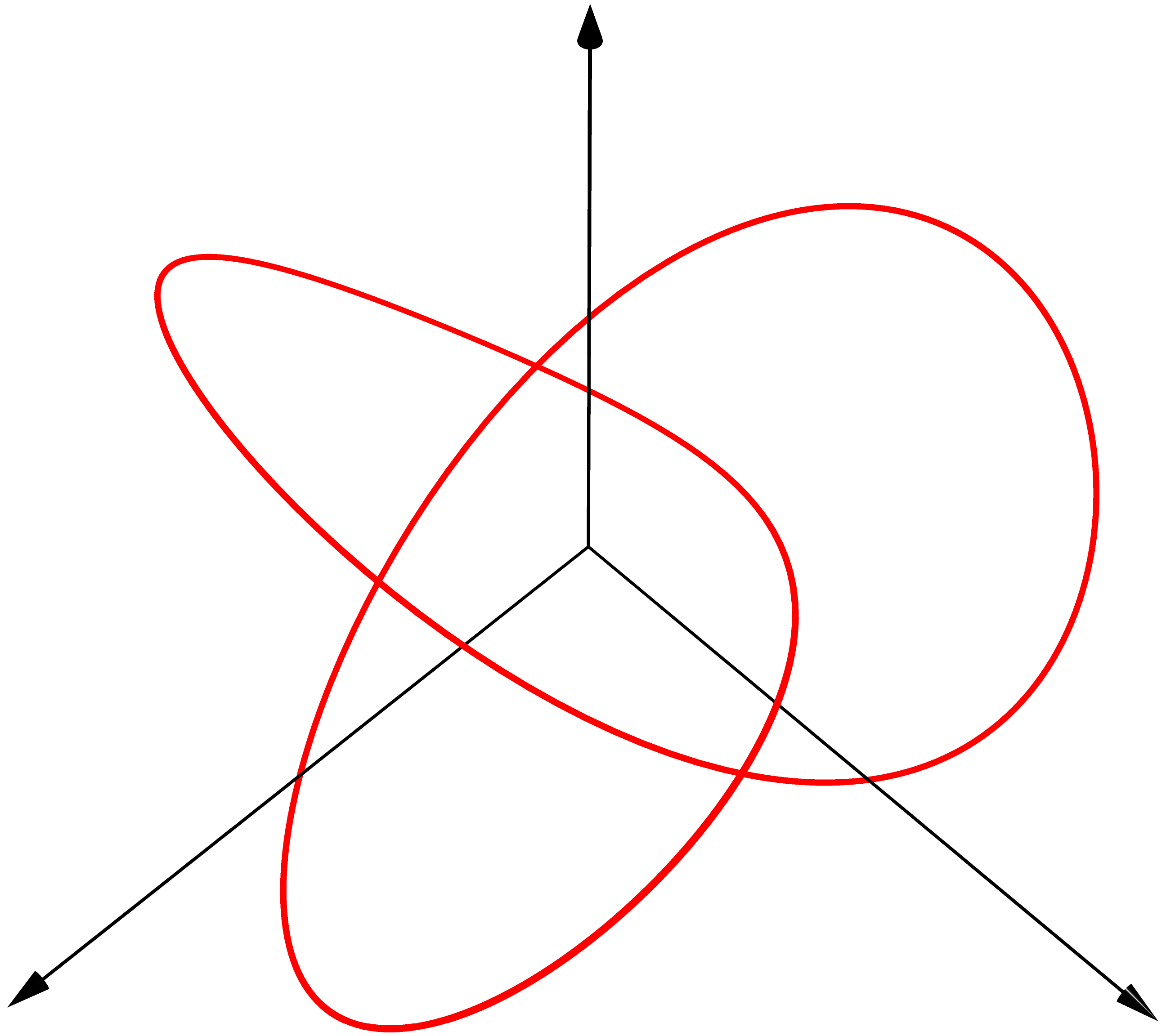
新規タブで開く
パラメータ表示された空間曲線を描くには次のように書きます。import threeの代わりにimport graph3という命令を使います。
settings.outformat="pdf";
settings.render=16;
settings.prc = false;
unitsize(1cm);
import graph3;
currentprojection=perspective(1,1,2);
triple F(real t) {return (sin(t)+2sin(2t),cos(t)-2cos(2t),-sin(3t));}
path3 C=graph(F,0,2pi, operator ..);
draw(C,red);
draw(O--4X, Arrow3(4));
draw(O--4Y, Arrow3(4));
draw(O--4Z, Arrow3(4));
定義済みの立体と空間における変換
球、円板、正方形、立方体、円柱、円錐面、円錐固体、半球などは標準的なものがあらかじめ定義されていて呼び出すだけで描くことができます。
単位球面unitsphereを描くには次のように書きます。
settings.outformat="pdf"; settings.render=16; settings.prc = false; unitsize(1cm); import three; draw(unitsphere,green);
円板を描くには次のように書きます。ここでscale3(1.2)*unitdiskは単位円板unitdiskを1.2倍に拡大するという命令です。
settings.outformat="pdf"; settings.render=16; settings.prc = false; unitsize(1cm); import three; draw(unitsphere,blue); draw(scale3(1.25)*unitdisk,white);
新規タブで開く
正方形を描くには次のように書きます。ここでshift((-1,-1,-1))*scale3(2)*unitplaneは単位正方形unitplaneを2倍に拡大したものをベクトル(-1,-1,-1)だけ平行移動するという命令です。
settings.outformat="pdf"; settings.render=16; settings.prc = false; unitsize(1cm); import three; draw(unitsphere,red); draw(shift(-1,-1,-1)*scale3(2)*unitplane,gray(0.3));
新規タブで開く
立方体を描くには次のように書きます。
settings.outformat="pdf"; settings.render=16; settings.prc = false; size(2cm,0); unitsize(1cm); import three; draw(unitcube,pink);
円柱を描くには次のように書きます。ここでshift((0,0,-1))*zscale3(1.5)*unitcylinderは単位円柱unitcylinderをz軸方向に1.5倍に拡大したものをベクトル(0,0,-1)だけ平行移動するという命令です。
settings.outformat="pdf"; settings.render=16; settings.prc = false; size(2cm,2cm); unitsize(1cm); import three; draw(shift(0,0,-1)*zscale3(1.5)*unitcylinder, surfacepen=material(green, emissivepen = gray(0.15)));
円錐側面を描くには次のように書きます。ここでzscale3(2)*unitconerは単位円錐unitconeをz軸方向に2倍に拡大するという命令です。
settings.outformat="pdf"; settings.render=16; settings.prc = false; unitsize(1cm); import three; currentprojection=perspective(1,0,-0.1); draw(zscale3(3)*unitcone,surfacepen=material(pink, emissivepen = gray(0.1)));
新規タブで開く
円錐(底面を込めたもの)を描くには次のように書きます。 ここでrotate(180,O,X)はO=(0,0,0)とX=(1,0,0)を通る直線、 つまりx軸のまわりに180度回転させるという命令です。
settings.outformat="pdf"; settings.render=16; settings.prc = false; unitsize(1cm); import three; currentprojection=perspective(1,1,0.3); draw(rotate(180,O,X)*zscale3(3)*unitsolidcone, surfacepen=material(green, emissivepen =gray(0.1)));
半球面を描くには次のように書きます。 ここでrotate(30,O,X-Y)はO=(0,0,0)とX-Y=(1,-1,0)を通る直線のまわりに30度回転させるという命令です。
settings.outformat="pdf"; settings.render=16; settings.prc = false; unitsize(1cm); import three; currentprojection=perspective(1,0,1/4); draw(rotate(30,O,X-Y)*unithemisphere, surfacepen=material(red, emissivepen =gray(0.2)));
単位球面をx軸方向に3倍に、y軸方向に2倍に拡大し、さらにx軸のまわりに15度回転させてから ベクトル(0,0,-2)により平行移動したもの曲面をsとし、これをxy平面に関して鏡映して得られる曲面をsprimeとします。 曲面sと曲面sprimeを描くには次のように書きます。 ここでreflect(p1,p2,p3)は3点p1、p2、p3を通る平面に関する鏡映(面対称移動)するという命令です。
settings.outformat = "pdf"; settings.render=16; settings.prc = false; unitsize(0.3cm); import three; currentprojection=perspective(2,1,0.2); surface s=shift(0,0,-2)*rotate(15,O,X)*yscale3(2)*xscale3(3)*unitsphere; surface sprime=reflect(O,X,Y)*s; path3 H = plane(8(1,0,0),8(0,1,0),(-4,-4,0)); draw(shift(-3,-3,-3)*scale3(6)*unitcube,surfacepen=white+opacity(0.1)); draw(s,red); draw(sprime,blue); draw(surface(H),surfacepen=pink);
平面
平面を描くには次のように書きます。ここでplane(v1,v2,p1)は点p1を通り,ベクトルv1とベクトルv2で張られる平行四辺形を与える命令です。path3 H1=plane(v1,v2,p1)はこの平行四辺形にH1という名前を付けています。surface(H1)はこの平行四辺形の面を表します。opacity(0.60)は不透明度60パーセントという意味です。
settings.outformat = "pdf"; settings.render=16; settings.prc = false; unitsize(1cm); import three; path3 H1 = plane((1,1,0),(0,2,1),(0,0,0)); draw(shift(-1/2,-3/2,-1/2)*surface(H1), surfacepen=cyan+opacity(0.60)); draw(O--X,Arrow3(4)); draw(O--Y,Arrow3(4)); draw(O--Z,Arrow3(4));
曲面
2変数関数のグラフ
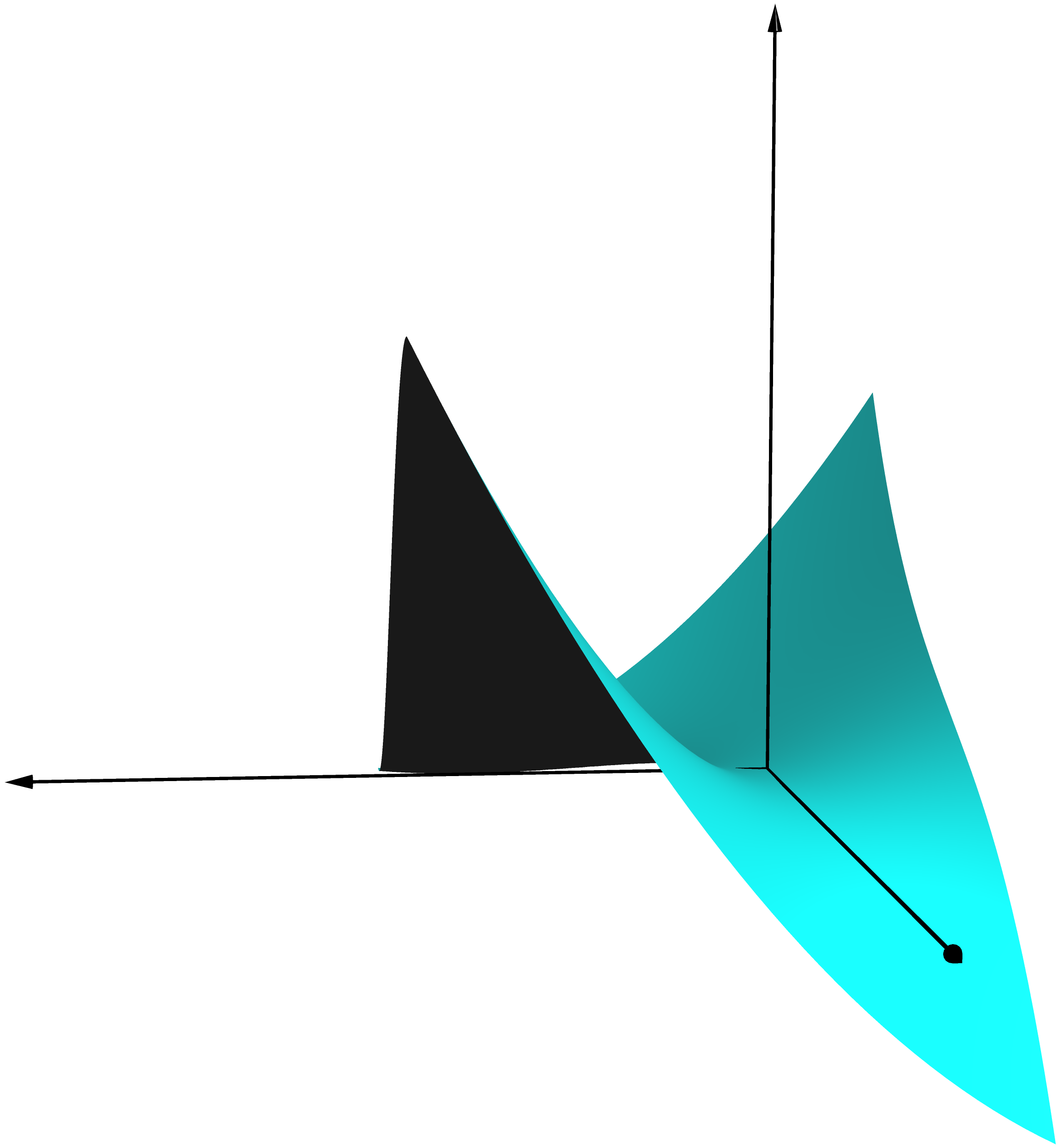
新規タブで開く
2変数
settings.outformat="pdf";
settings.render=16;
settings.prc = false;
unitsize(1cm);
import graph3;
currentprojection=perspective((1,5,1));
real F(pair t) {real x = t.x; real y = t.y;
return x*y+x^2/2-y^3/3;}
surface S=surface(F,(-1/2,-1),(1,1), Spline);
draw(S,surfacepen=material(cyan, emissivepen=0.2 gray));
draw(O--2X, Arrow3(4));
draw(O--2Y, Arrow3(4));
draw(O--2Z, Arrow3(4));
新規タブで開く
回転面を描くには次のように書きます。ここでsurface(p,C,v)は既に定義されている空間曲線Cを、 点pを通る方向ベクトルvの直線を回転軸として回転させて得られる回転面を描く命令です。
settings.outformat="pdf";
settings.render=16;
settings.prc = false;
size(2cm);
import graph3;
triple f1(real t) {return (2+cos(t),sin(t),0);}
path3 C1=graph(f1,0,2pi, operator ..);
surface S1 = surface((0,0,0),C1,(0,1,0));
draw(S1,surfacepen=material(red, emissivepen=0.2 red));
新規タブで開く
錐の側面を描くには次のように書きます。ここでextrude(C,p -- cycle)は頂点pから既に定義されている空間曲線C上の点qを結んで得られる錐面を与える命令です。
settings.outformat="pdf";
settings.render=16;
settings.prc = false;
size(2cm);
import graph3;
triple f1(real t) {return (1+cos(t),sin(t),0);}
path3 C1=graph(f1,0,2pi, operator ..);
draw(extrude(C1,(0,0,2) -- cycle), material(gray,emissivepen=0.2 red));
新規タブで開く
柱の側面を描くには次のように書きます。ここでextrude(C,v)は既に定義されている空間曲線Cを底、vを高さ方向のベクトルとした柱の側面を与える命令です。
settings.outformat="pdf";
settings.render=16;
settings.prc = false;
size(2cm);
import graph3;
triple f1(real t) {return (1+cos(t),sin(2t),0);}
path3 C1=graph(f1,0,2pi, operator ..);
draw(extrude(C1,(0,1,-1)), material(cyan,emissivepen=0.2 gray));
新規タブで開く
パラメータ表示された曲面を描くには次のように書きます。
settings.outformat = "pdf";
settings.render=16;
settings.prc = false;
unitsize(0.6cm);
import graph3;
currentprojection=perspective(1,2,1);
// currentprojection=orthographic((5,2,3));
triple F(pair t) {real u = t.x; real v = t.y;
return (u-u^3/3+u*v^2,-v+v^3/3-u^2*v,u^2-v^2);}
surface S=surface(F,(-1,-1),(1,1), Spline);
draw(S,surfacepen=pink);
新規タブで開く
方程式で定義された曲面を描くには次のように書きます。
settings.outformat="pdf";
settings.render=16;
settings.prc = false;
unitsize(1cm);
import smoothcontour3;
real f1(real x, real y, real z) {
return x^2+2y^2+3z^2-1;}
surface S1=implicitsurface(f1,(-1,-1,-1),(1,1,1),
overlapedges=true,nx=20, nz=5);
draw(S1,surfacepen=yellow);
新規タブで開く
方程式で定義された曲面の例をもう1つ挙げておきます。
settings.outformat="pdf";
settings.render=16;
settings.prc = false;
unitsize(0.4cm);
import smoothcontour3;
currentprojection=orthographic((5,3,3));
real R=1.2, r=1/2, a=sqrt(2);
real f1(real x, real y, real z) {
return -a^2 + ((-r^2 + R^2)^2 -
2 (r^2 + R^2)*((-r - R + x)^2 + y^2) + 2 (-r^2 + R^2)*z^2
+ ((-r - R + x)^2 + y^2 + z^2)^2)*((-r^2 + R^2)^2
- 2 (r^2 + R^2)*((r + R + x)^2 + y^2)
+ 2 (-r^2 + R^2)*z^2 + ((r + R + x)^2 + y^2 + z^2)^2);}
surface S1=implicitsurface(f1,(-2 (r + R),-(r + R),-r - a),
(2 (r + R),(r + R),r + a), overlapedges=true,nx=20, nz=5);
draw(S1,surfacepen=green);
空間の点を折線・曲線で結ぶ
新規タブで開く
空間におけるいくつかの点を折線で結ぶには次のように書きます。
settings.outformat = "pdf"; settings.render=16; settings.prc = false; unitsize(1cm); import graph3; real r=3*sqrt(2)/4; triple p0=(1,0,0),p1=(-1/2,sqrt(3)/2,0), p2=(-1/2,-sqrt(3)/2,0), p3=(0,0,sqrt(2)); path3 c0=p0 -- p1 -- p2 -- cycle; path3 c1=p3 -- p0 -- p1; path3 c2=p3 -- p1 -- p2; path3 c3=p3 -- p2 -- p0; draw(c0, linewidth(1pt)); draw(c1, linewidth(1pt)); draw(c2, linewidth(1pt)); draw(c3, linewidth(1pt)); dot(p0,red); dot(p1,red); dot(p2,red); dot(p3,red); draw(shift(0,0,sqrt(2)/4)*scale3(r)*unitsphere, surfacepen=yellow+opacity(0.40),render(compression=Low,merge=true));
新規タブで開く
空間におけるいくつかの点を曲線で結ぶには次のように書きます。
settings.outformat = "pdf"; settings.render=16; settings.prc = false; unitsize(1cm); import graph3; real r=3*sqrt(2)/4; triple p0=(1,0,0),p1=(-1/2,sqrt(3)/2,0), p2=(-1/2,-sqrt(3)/2,0), p3=(0,0,sqrt(2)); path3 c0=p0 .. p1 .. p2 .. cycle; path3 c1=p3 .. p0 .. p1; path3 c2=p3 .. p1 .. p2; path3 c3=p3 .. p2 .. p0; draw(c0, linewidth(1pt)); draw(c1, linewidth(1pt)); draw(c2, linewidth(1pt)); draw(c3, linewidth(1pt)); dot(p0,red); dot(p1,red); dot(p2,red); dot(p3,red); draw(shift(0,0,sqrt(2)/4)*scale3(r)*unitsphere, surfacepen=cyan+opacity(0.40),render(compression=Low,merge=true));