整数論のいくつかのトピックスについて解説します．

1次不定方程式

二つの自然数 $a, b$ の最大公約数を $\gcd(a,b)$ とかくことにする．$a$ を $b$ で割ったときの商を $q$，余りを $r$ とする． \[ a=bq+r, \qquad 0 \leq r < b.\] また，$\gcd(a,b)=\gcd(b,r)$ であることが容易にわかる．$r > 0$ ならば，$b$ を $r$ で割ったときの商を $q_1$，余りを $r_1$ とする． \[ b=rq_1+r_1.\] そのとき，$\gcd(a,b)=\gcd(b,r)=\gcd(r,r_1)$ である．これを繰り返せば，余りは $0$ 以上であり単調に減少するから，いつかは割り切れてしまう．そのときの，割り切る数が $\gcd(a,b)$ と等しい．このようにして最大公約数を計算できる．これをユークリッドの互除法 という．また，この計算を逆にたどれば，$d=\gcd(a,b)$ とおくとき， \[ ax+by=d\] を満たす整数 $x, \,y$ を求めることができる．

具体例で説明しよう．$209$ と $87$ の最大公約数を求める． \begin{align*} 209 &= 87 \times 2 + 35,\\ 87 &= 35 \times 2 + 17, \\ 35 &= 17 \times 2 + 1,\\ 17 &= 1 \times 17. \end{align*} これから，$\gcd(209,87)=1$ となる．これを書き直して， \begin{align*} 1 &= 35 - 17 \times 2 \\ &= 35 - (87 - 35 \times 2) \times 2 \\ &= 35 \times 5 - 87 \times 2 \\ &= (209 - 87 \times 2) \times 5 - 87 \times 2 \\ &= 209 \times 5 - 87 \times 12. \end{align*} したがって，$x=5, \; y=-12$ は不定方程式 \[ 209x+87y=1\] の一つの整数解である．一般解を求めよう． \begin{gather*} 209(x - 5) + 87(y + 12) = 0, \\ 209(x - 5) = -87(y + 12) \end{gather*} より，$x - 5 = 87t,\; y+12 = -209t$, $t$ は任意の整数とかける． すなわち，一般解は \[ x= 5 + 87t, \quad y= -12 - 209t, \quad t \in \mathbb{Z}\] によって与えられる．

ペル方程式

$m$ を平方数でないような自然数とするとき，不定方程式 \[ x^2-my^2=1\] をペル方程式 という．ペル方程式は無数の整数解を持つことことが知られている．解の求め方を説明しよう．

実数 $x$ に対して，$x$ の整数部分と小数部分を次の記号で表す． \[ x=[x]+\{x\}, \qquad [x] \in \mathbb{Z},\; 0 \leq \{x\} < 1.\] 整数からなる数列 $\{q_n\}$ と無理数からなる数列 $\{x_n\}$ を次のように定義する． \begin{align*} x_0&=[\sqrt{m}]+\sqrt{m}, \\ q_n&=[x_n], \quad x_{n+1}=\frac{1}{\{x_n\}}=\frac{1}{x_n-q_n},\;\; n=0,1,2,\dots. \end{align*} そのとき，ある番号 $N$ が存在して，$x_N=x_0$ となる． \[ x_n=[x_n]+\{x_n\}=q_n+\frac{1}{x_{n+1}} \] であるから，この式を $n = N-1, N-2, \dots, 0$ について用いれば， \[ x_0=\frac{ax_0+b}{cx_0+d} \] を得る．ここで，$a, b, c, d$ は自然数で \[ad - bc = (-1)^N \] を満たしている．したがって，$x_0$ は2次方程式 \[ cx_0^2+(d-a)x_0-b=0 \] を満たす．一方，$t = [\sqrt{m}]$ とおけば，定義から，$x_0$ は2次方程式 \[ x_0^2-2t x_0+t^2-m=0 \] を満たす．これらの二つの2次方程式を比較して， \[ d-a=-2ct, \quad -b=c(t^2-m) \] を得る．これと $ad - bc = (-1)^N$ より， \begin{gather*} a(a-2ct)+c^2(t^2-m)=(-1)^N,\\ (a-ct)^2-mc^2=(-1)^N. \end{gather*} すなわち，$x = a-ct$, $y=c$ は \[ x^2-my^2=(-1)^N \] の整数解である．

以上の方法を $m=19$ の場合に適用してみよう． $t=[\sqrt{19}]=4$ である． \begin{align*} x_0 &= 4 + \sqrt{19}, \quad q_0 = [x_0] = 8, \\ x_1 &= \frac{1}{-4 + \sqrt{19}} = \frac{4 + \sqrt{19}}{3}, \quad q_1 = [x_1] = 2,\\ x_2 &= \frac{3}{-2 + \sqrt{19}} = \frac{2 + \sqrt{19}}{5}, \quad q_2 = [x_2] = 1, \\ x_3 &= \frac{5}{-3 + \sqrt{19}} = \frac{3 + \sqrt{19}}{2}, \quad q_3 = [x_3] = 3, \\ x_4 &= \frac{2}{-3 + \sqrt{19}} = \frac{3 + \sqrt{19}}{5}, \quad q_4 = [x_4] = 1, \\ x_5 &= \frac{5}{-2 + \sqrt{19}} = \frac{2 + \sqrt{19}}{3}, \quad q_5 = [x_5] = 2, \\ x_6 &= \frac{3}{-4 + \sqrt{19}} = 4 + \sqrt{19} = x_0. \end{align*} したがって， \[ x_n = q_n + \frac{1}{x_{n+1}} \] を $n = 5, 4, 3, 2, 1, 0$ の順に計算すれば， \begin{align*} x_5 &= 2 + \frac{1}{x_0} = \frac{2x_0 + 1}{x_0}, \\ x_4 &= 1 + \frac{x_0}{2x_0 + 1} = \frac{3x_0 + 1}{2x_0 + 1}, \\ x_3 &= 3 + \frac{2x_0 + 1}{3x_0 + 1} = \frac{11x_0 + 4}{3x_0 + 1}, \\ x_2 &= 1 + \frac{3x_0 + 1}{11x_0 + 4} = \frac{14x_0 + 5}{11x_0 + 4}, \\ x_1 &= 2 + \frac{11x_0 + 4}{14x_0 + 5} = \frac{39x_0 + 14}{14x_0 + 5}, \\ x_0 &= 8 + \frac{14x_0 + 5}{39x_0 + 14} = \frac{326x_0 + 117}{39x_0 + 14}. \end{align*} よって，$a = 326, b = 117, c = 39, d = 14$ とおけば， \[ x= a - ct = 326 - 39\times 4 = 170, \quad y = c = 39.\] これはペル方程式 $x^2-19y^2=1$ の整数解である． $n = 1, 2, \dots$ に対して，自然数 $x_n, y_n$ を \[ (170 + 39\sqrt{19})^n=x_n+y_n\sqrt{19}\] によって定めれば，これらはペル方程式 \[ x^2-19y^2=1 \] の整数解である．実はこれらがこの方程式の自然数解のすべてである．また，$x_n$, $y_n$ は次の漸化式によって計算できる． \begin{align*} x_1 &= 170, \quad y_1= 39, \\ x_{n+1} &= 170x_n+ 741y_n, \\ y_{n+1} &= 39x_n+170y_n. \end{align*}

2元2次形式

$a, b, c$ を整数とするとき，$x$, $y$ を変数とする2次式 \[ f(x,y) = ax^2+bxy+cy^2 \] を2元2次形式 という．$D = b^2-4ac$ を $f(x,y)$ の判別式 という． $a>0$ かつ $D<0$ ならば，$(x,y)$ が $(0,0)$ と異なる値をとるとき $f(x,y)>0$ である．このとき，$f(x,y)$ は 正定値 であるという．整数 $p, q, r, s$ が $ps - qr = 1$ を満たすとき， \[ g(x,y)=f(px + ry, qx + sy) = a'x^2+b'xy+c'y^2 \] とおけば，$g(x,y)$ も正定値2元2次形式である．$g(x,y)$ の判別式は $f(x,y)$ の判別式と等しい．また，$f(x,y)$ と $g(x,y)$ がこのような関係であるとき，$f(x,y)$ と $g(x,y)$ は同値 であるという．与えられた負の整数 $D$ を判別式として持つ正定値2元2次形式は $0 < a < c, -a<b \leq a$ または $0<a=c, 0 \leq b \leq a$ を満たす2元2次形式 $f(x,y)=ax^2+bxy+cy^2$ と同値である． このとき， \[ |D|= 4ac - b^2 \geq 3a^2\] であるから，同値類の数は有限であることがわかる．この数を $D<0$ の類数という．

与えられた正の整数 $D$ を判別式として持つ2元2次形式は \[a>0, \quad c< 0, \quad a+b+c< 0, \quad a-b+c< 0 \] を満たす2元2次形式 $f(x,y)=ax^2+bxy+cy^2$ と同値である．このとき， \[D = b^2-4ac>b^2\] であるから，$b$ のとる値は有限であり，各 $b$ の値に対して，$D = b^2-4ac$ より， $a$ と $c$ のとる値も有限である．したがって，同値類の数も有限であることがわかる．この数を $D>0$ の類数 という．

2つの平方の和にかける素数

素数 $p$ が整数 $x, y$ を用いて \[ p=x^2+y^2 \] とかけるのはいつだろうか．まず，$2$ は $2 = 1^2+1^2$ とかける．$p$ を奇素数とする．$p = x^2+y^2$ とかけたとする．$x$, $y$ ともに偶数でも，$x$, $y$ ともに奇数でも，$x^2+y^2$ は偶数となるから，$x$, $y$ の一つは奇数でもう一つは偶数である． $x = 2x_1+1$, $y=2y_1$ とかけば， \[ p = 4x_1^2+4x_1+1+4y_1^2 \] であるから，$p$ を $4$ で割った余りは $1$ である．逆に，$p$ を $4$ で割った余りは $1$ であるとする．ウィルソンの定理によって，$(p - 1)! + 1$ は $p$ で割り切れる．$X = ((p - 1)/2)!$ とおくと， \[ (p - 1)! + 1 = (p - 1)(p - 2) ... ((p + 1)/2) X + 1.\] ここで， \begin{align*} (p - 1)(p - 2) ... ((p + 1)/2) &= (p - 1)(p - 2) \cdots (p - (p - 1)/2) \\ &= (-1)^{(p - 1)/2}X + (p \text{の倍数}) \end{align*} であり，$(-1)^{(p - 1)/2}=1$ であるから，$X^2+1$ は $p$ の倍数である．よって，2つの平方数の和で $p$ の倍数になるものが存在する． $x^2+y^2=pm$ とする．$m = 1$ ならば $p$ は2つの平方の和にかけている．$m > 1$ とする．$x$ を $m$ で割った余りを $a$ とし，$y$ を $m$ で割った余りを $b$ とする．さらに，$a > m/2$ ならば，$a$ を $a - m$ で置き換える．同様に，$b > m/2$ ならば，$b$ を $b - m$ で置き換える．このとき，$bx - ay$ と $ax + by$ はともに $m$ の倍数であるから， \[x_1 = \frac{bx- ay}{m}, \quad y_1=\frac{ax + by}{m} \] とおけば， \[ x_1^2+y_1^2=\frac{(a^2+b^2)(x^2+y^2)}{m^2}=\frac{(a^2+b^2)p}{m}\] である．ここで，$a^2+b^2$ は $m$ の倍数であり， \begin{align*} a^2+b^2&\leq \left(\frac{m}{2} \right)^2+\left(\frac{m}{2} \right)^2=\frac{m^2}{2},\\ m'&=\frac{a^2+b^2}{m} \leq \frac{m}{2} \end{align*} である．よって，$x_1^2+y_1^2=pm', \;m'<m/2$ である．これを繰り返せば，$p$ が2つの平方の和にかけることがわかる．

ピタゴラス数

四千年前のバビロニアにおいて，三辺の長さ $X, Y, Z$ が整数であるような直角三角形として，$X, Y, Z$ が次のようなものが知られていた．

これらは不定方程式 \[ X^2+Y^2=Z^2 \] の整数解である．ピタゴラスは紀元前6世紀頃，この不定方程式の整数解として， \[ X= 2a + 1, \quad Y = 2a^2+2a, \quad Z = 2a^2+2a+1 \] を与えた．7世紀頃，インドのブラマグプタは一般解 \[ X = a^2-b^2, \quad Y=2ab, \quad Z=a^2+b^2 \] に到達していた．

フェルマー予想

17世紀のフランスの数学者フェルマーは，愛読書の余白に次のような書き込みをした．

平方より大きいべきを2つの同一のべきに分かつことはできない．そのことの真に驚くべき証明を見つけたが，この余白は狭すぎ て書けない．

これを現代の記法でかけば，次のようになる．$n$ を3以上の自然数とすると， \[ X^n+Y^n=Z^n\] を満たす自然数 $X, Y, Z$ は存在しない．これが有名なフェルマーの最終定理 ，あるいはフェルマーの大定理 と呼ばれるものである．

フェルマーは，自分が見つけた定理を他国の数学者に手紙で知らせた．$n = 3, 4$ の場合を手紙に書いているだけで，それ以外の場合にはふれていない．$n = 4$ の場合の彼の証明は復元されているが，$n = 3$ の場合の証明は残されていない．また，彼の他の書き物や，当時のレベルから見ても一般の場合の証明ができていたとは考えられない．このような理由から，上の命題はフェルマー予想 と呼んだ方が適切であった．

フェルマー以降，19世紀中頃までに，この問題には次のような進展があった．

• 1770年　オイラー(スイス)　$n = 3$ の場合を証明．
• 1825年　ディリクレ(ドイツ) $n = 5$ の場合を証明．
• 1847年　クンマー(ドイツ)　十分条件を与える．

クンマーの得た結果は，個々の $n$ について問題を考えるのではなく，予想が正しいための $n$ の十分条件を，具体的に計算できる形で与えているという点で画期的であった．また，彼の仕事を一般化することによって，代数的整数論 という分野が発達したことの意義は非常に大きいと考えられる．20世紀に入って，整数論は著しく発達し，遂に1994年にワイルスは20世紀の整数論の成果の総力を結集して，この予想を解決した．人類は一つの整数論の問題を約350年かけて考え続け，解決に成功したのである．

代数体

方程式 \[ x^2+y^2=z^2 \] を考える．この方程式の整数解はピタゴラス数 と呼ばれる．もし，複素数 $i$, $i^2=-1$, を用いれば，この方程式の右辺を次のように因数分解できる． \[ (x+yi)(x-yi)=z^2. \] これから，我々はガウスの整数環 \[ \mathcal{O} = \{ x + yi : x, y \in \mathbb{Z} \}\] に導かれる．環 $\mathcal{O}$ は通常の整数のなす環 $\mathbb{Z}$ と同様な性質を持っている．$\mathcal{O}$ の元は $\mathcal{O}$ における素数 の積として一意的に表せることが証明できる．

もし，三個の整数 $A$, $B$, $C$ について，$A$ と $B$ が $1$ より大きい公約数を持たず，さらに， \[ AB = C^2 \] ならば $A$ と $B$ は両方とも平方数であることが素因数分解の一意性からわかる．同様に，もし $x$, $y$, $z$ がピタゴラス数であり， $x$ と $y$ が $1$ より大きい公約数を持たなければ，$x + yi$ と $x - yi$ はともに，$\mathcal{O}$ における平方数でなければならないことがわかる．また，$x$ と $y$ のうち一方が奇数で他方が偶数であることがわかる．$x$ が奇数で $y$ が偶数であるとする．そのとき， \[ x + yi = (a + bi)^2=a^2-b^2+2abi \] したがって， \[ x=a^2-b^2, \quad y=2ab, \quad z=a^2+b^2 \] を得る．このようにガウスの整数環のような環を考えることは，通常の整数に関する多く問題に対して非常に役に立つ．そのような環は代数体の整数環 と呼ばれる．

代数的数 とは，有理数係数の代数方程式 \[ x^n+a_1x^{n-1}+\cdots+a_{n-1}x+a_n=0, \quad a_i \in \mathbb{Q} \] の根であるような複素数である．代数的整数 とは，最高次の係数が$1$であるような整数係数の代数方程式> \[ x^n+a_1x^{n-1}+\cdots+a_{n-1}x+a_n=0, \quad a_i \in \mathbb{Z} \] の根であるような複素数である．(有限次)代数体 $K$ とは，有理数体 $\mathbb{Q}$ 上有限次元のベクトル空間であるような複素数体 $\mathbb{C}$ の部分体である．代数体 $K$ は次のような形に表せる． \[ K=\{c_0+c_1\theta+\cdots+c_{n-1}\theta^{n-1}: c_j \in \mathbb{Q} \}. \] ここで，$\theta$ はある代数的数である．$K$ の整数環 とは，$K$ に属する代数的整数の全体のなす環である．それを $\mathcal{O}_K$ で表す．環 $\mathcal{O}_K$ においては，一般には素因数分解の一意性は成立しない．しかし，それが素因数分解の一意性とどれくらい離れているかを測る不変量が存在する．その不変量は代数体 $K$ の類数 と呼ばれる．

$K$ が 2次方程式 $x^2+m=0$, $m$ は平方因数を持たない正整数，によって定義される虚2次体 のとき， \[ D=\left\{ \begin{array}{ll} -m , &\quad \text{$m$ を $4$ で割った余りが $3$}, \\ -4m , &\quad \text{$m$ を $4$ で割った余りが $1$ か $2$} \end{array} \right. \] とおく．そのとき，$K$ の類数は，判別式 $D$ の正定値2元2次形式の類数と等しい．

自然数の負べき乗の無限和

次のような無限級数の和は容易に求められる． \begin{align*} \sum_{n=0}^\infty r^n&=1+r+r^2+\cdots =\frac{1}{1-r}, \quad |r|< 1, \\ \sum_{n=1}^\infty \frac{1}{n(n+1)} &=\frac{1}{1\cdot 2}+\frac{1}{2\cdot 3}+\frac{1}{3\cdot 4}+\cdots=1. \end{align*} これに対して，次の無限級数の和はそう簡単には求められない． \[ \sum_{n=1}^\infty \frac{1}{n^2}=\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots. \] この和を最初に求めたのは，オイラーである．オイラーは1735年に \[ \sum_{n=1}^\infty \frac{1}{n^2}=\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots=\frac{\pi^2}{6} \tag{$*$}\] であることを発見した．この不思議な公式を発見したとき，オイラーはその喜びを次のように述べている．

私は何度試みても，それらの和に対する近似値しか得られませんでした．しかるに，今回まったく思いもかけず，この和に対する優雅な公式が発見できました．それは円周率に関係しているのです．

左辺をいくらながめても影も形もない円周率 $\pi$ がどうして右辺に現れるのか？オイラーがどのようにしてこの等式を発見したかを説明しよう．まず，三角関数 $\sin x$ は次のようなテイラー展開を持つ． \[ \sin x= x - \frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots.\] また，$x$ の $n$ 次多項式 $f(x)$ が $x = a_1, \dots, a_n$ で $0$ になれば， \[ f(x) = b(x - a_1) \cdots (x - a_n) \] と因数分解できる．$\sin x$ は $x$ の多項式でないが，$x = n\pi$, $n= 0, \pm 1, \pm 2, \pm 3, \dots$ で $0$ になるから，無限積 \[ bx(x - \pi)(x + \pi)(x - 2\pi)(x + 2\pi) \cdots \] として表せないだろうか．しかし，この無限積は収束しないことは容易にわかる．そこで，少し修正して \begin{align*} & \quad bx\left(1 - \frac{x}{\pi}\right)\left(1 + \frac{x}{\pi}\right)\left(1 - \frac{x}{2\pi}\right)\left(1 + \frac{x}{2\pi}\right) \cdots \\ &= bx\left(1 - \frac{x^2}{\pi^2}\right)\left(1 - \frac{x^2}{4\pi^2}\right)\left(1 - \frac{x^2}{9\pi^2}\right) \cdots \\ &=bx \prod_{n=1}^\infty \left(1 - \frac{x^2}{n^2\pi^2}\right) \end{align*} を考える．これは収束して，$x= n\pi$, $n = 0, \pm 1, \pm 2, \pm 3, \dots$ で $0$ になる関数を表す．この関数を $g(x)$ とする．もし，$\sin x=g(x)$ になったとすれば， \[ 1 = \lim_{n \rightarrow 0} \frac{\sin x}{x} =\lim_{n \rightarrow 0} \frac{g(x)}{x}=b \] より，$b = 1$ である．実際に， \[ \sin x=x \prod_{n=1}^\infty \left(1 - \frac{x^2}{n^2\pi^2}\right)=x\left(1 - \frac{x^2}{\pi^2}\right)\left(1 - \frac{x^2}{4\pi^2}\right)\left(1 - \frac{x^2}{9\pi^2}\right) \cdots \] が成り立つことが証明される．これを $sin\,x$ の無限積展開 という．オイラーは $\sin x$ の無限積展開のかけ算を展開して得られる級数と $\sin x$ のテイラー展開の $x^3$ の係数を比較することによって，自然数の平方の逆数の無限和の値が $\pi^2/6$ であることを発見した．さらに，オイラーは $x^5, x^7, \dots$ の係数を比較することによって， \begin{align*} \sum_{n=1}^\infty \frac{1}{n^4}&=\frac{1}{1^4}+\frac{1}{2^4}+\frac{1}{3^4}+\cdots=\frac{\pi^4}{90}, \\ \sum_{n=1}^\infty \frac{1}{n^6}&=\frac{1}{1^6}+\frac{1}{2^6}+\frac{1}{3^6}+\cdots=\frac{\pi^6}{945}, \\ \sum_{n=1}^\infty \frac{1}{n^8}&=\frac{1}{1^8}+\frac{1}{2^8}+\frac{1}{3^8}+\cdots=\frac{\pi^8}{9450}, \\ \sum_{n=1}^\infty \frac{1}{n^{10}}&=\frac{1}{1^{10}}+\frac{1}{2^{10}}+\frac{1}{3^{10}}+\cdots=\frac{\pi^{10}}{935550}, \\ \sum_{n=1}^\infty \frac{1}{n^{12}}&=\frac{1}{1^{12}}+\frac{1}{2^{12}}+\frac{1}{3^{12}}+\cdots=\frac{691\pi^{12}}{638512875} \end{align*} を求めた．一般に $k$ を正の偶数とすれば， \[ \zeta(k)=\sum_{n=1}^\infty \frac{1}{n^k}=\frac{1}{1^k}+\frac{1}{2^k}+\frac{1}{3^k}+\cdots=(\text{有理数})\times \pi^k \] であることがわかる．このようにして，オイラーは等式 $(*)$ を発見したが，多項式の因数分解を $\sin x$ のような関数にも適用してしまうオイラーの大胆な発想は当時の数学者達からも疑念を持たれた．しかし，オイラー本人はこの議論によって結論されるこれらの和の値が以前に数値計算して得られたものとぴったり合っていることから，それらの値が正しいことを確信していた．発見から10年後の1745年にオイラーは無限積展開についても証明を与えている．

正の偶数 $k$ に対する $\zeta(k)$ の公式に現れる有理数は，ベルヌイ数 を用いて表すことができる．それは，円分体の類数と密接に関係して，フェルマー予想に関するクンマーの仕事において重要な役割を果たした．また，$k$ が $3$ 以上の奇数のときには，この和がどんな数であるかはほとんど知られていない．アペリーによって，$k = 3$ のときの和が無理数であることが証明されたのは，1978年のことである．

実数 $s > 1$ の関数 $\zeta(s)$ を収束する無限級数 \[ \zeta(s)=\sum_{n=1}^\infty \frac{1}{n^s}=\frac{1}{1^s}+\frac{1}{2^s}+\frac{1}{3^s}+\cdots \] によって定義する．これは $1$ 以外のすべての複素数 $s$ の関数に拡張される．これをリーマンのゼータ関数 という．リーマンのゼータ関数の解析的性質は，素数の分布と密接に関係している．リーマンのゼータ関数の自明でない零点はすべて $\Re(s)=1/2$ という直線上にあるという主張が，リーマン予想 と呼ばれる未解決の大問題である．

楕円曲線

不定方程式 $X^2+Y^2=Z^2$ の整数解を決定することは，円 $x^2+y^2=1$ の有理点を決定することと同じである．楕円や双曲線等の2次方程式で定義される曲線についても，円の場合と同様に扱える．次に問題になる曲線は， $a$, $b$, $c$ を整数として，方程式 \[E: y^2=x^3+ax^2+bx+c \] で表されるものである．ここで，3次方程式 \[ x^3+ax^2+bx+c=0 \] が重根を持たない場合が重要である．そのような曲線 $E$ を楕円曲線 という． 楕円曲線 $E$ 上の点の全体は，次のような演算によって無限遠点 $\infty$ を単位元とするアーベル群をなす．$E$ 上の2点 $P$, $Q$ に対して，$P$ と $Q$ を結ぶ直線と楕円曲線 $E$ とのもう一つの交点を $R$ とし，$x$-軸に関して $R$ と対称な点を $R'$ とするとき， \[ P+Q=R' \] と定義する．$R$ の逆元は $- R = R'$ である．

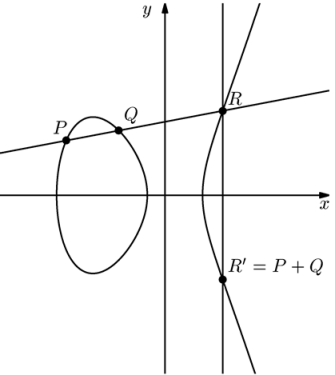
$P$, $Q$, $R$ の座標を \[ P = (x_1,y_1)，\quad Q= (x_2, y_2)，\quad R = (x_3, y_3) \] として，$x_1\neq x_2$のとき \[ \lambda = \frac{y_2-y_1}{x_2-x_1} \] とおく．直線 $PQ$ の方程式 \[ y = \lambda (x - x_1) + y_1 \] を $E$ の方程式に代入すれば \begin{gather*} (\lambda (x - x_1) + y_1)^2=x^3+ax^2+bx+c, \\ x^3+(a-\lambda^2)x^2+b'x+c'=0 \end{gather*} を得る．$x = x_1, x_2, x_3$ はこの 3次方程式の 3根だから，根と係数の関係によって， \[ x_1 + x_2 + x_3 = \lambda^2-a \] となる．したがって， \begin{align*} x_3&=\lambda^2-a-x_1-x_2, \\ y_3&=\lambda(x_3-x_1)+y_1 \end{align*} を得る．この等式から，$P$, $Q$ の $x, y$-座標がともに有理数ならば，$P + Q$ の $x, y$-座標も有理数であることがわかる．したがって，$E(\mathbb{Q})$ を $E$ 上の有理点全体の集合に無限遠点 $\infty$ を付け加えた集合とすれば，$E(\mathbb{Q})$ はアーベル群になる．

モーデルは $E(\mathbb{Q})$ の有限個の点 $P_1,\dots, P_r$ が存在して，任意の $E(\mathbb{Q})$ の点 $P$ は， \[ P = P_0+ n_1P_1+ \cdots+ n_rP_r, \quad n_1, \dots, n_r \in \mathbb{Z}, \] $P_0$ は有限位数の点，と表せることを証明した．この $r$ を楕円曲線 $E$ のランク という．ランクについては，Birch と Swinerton-Dyer による予想がある．また，Wiles によるフェルマー予想の解決も楕円曲線を用いている．

合同数問題

三辺の長さが有理数である直角三角形の面積となるような正の有理数 $r$ を合同数 という．すなわち， \[ X^2+Y^2=Z^2, \quad \frac{1}{2}XY=r \] を満たすような正の有理数 $X$, $Y$, $Z$ が存在するとき，$r$ は合同数であるという．例えば，三辺の長さが $3$,$4$,$5$ の直角三角形の面積は $6$ であるから，$6$ は合同数である．三辺の長さが $5$,$12$,$13$ の直角三角形の面積 $30$ も合同数である．また，三辺の長さが $24/5$, $35/12$, $337/60$ の直角三角形の面積 $7$ も合同数である．

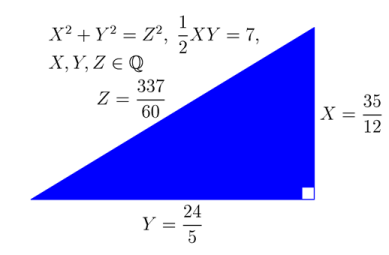
正の有理数 $X$, $Y$, $Z$ が \[ X^2+Y^2=Z^2, \quad \frac{1}{2}XY=r \] を満たせば，点 $(X/Z, Y/Z)$ は単位円の第$1$象限の有理点であるから，有理数 $t$ を用いて， \[ \frac{X}{Z}=\frac{1-t^2}{1+t^2}, \quad \frac{Y}{Z}=\frac{2t}{1+t^2} \] と表せる．したがって， \[ Z = s(1+t^2), \quad X=s(1-t^2), \quad Y=2st \] とかける．ここで，$s$, $t$ は有理数で， $s> 0$, $0 < t < 1$ である．そのとき，$X$, $Y$, $Z$ を三辺とする直角三角形の面積 $r$ は， \[ r = \frac{1}{2}XY = s^2t(1-t^2) \] で与えられる． $s$, $t$ にいろいろな有理数の値を与えることによって， 合同数が次々に得られる． 例えば，$t= 4/5$, $s = 25/6$ とおけば， \[ X = \frac{3}{2}, \quad Y=\frac{20}{3},\quad Z = \frac{41}{6}, \quad r = 5\] であり，$t = 9/16$, $s = 64/15$ とおけば， \[ X = \frac{35}{12}, \quad Y= \frac{24}{5}, \quad Z = \frac{337}{60}, \quad r = 7\] である．定義から，$r$ が合同数ならば，任意の正の有理数 $u$ について， $u^2r$ も合同数である．特に，$r = b/a$ と既約分数の形にかき，さらに，$a = a_0^2a_1$, $b = b_0^2b_1$, $a_0$, $b_0$ は自然数，$a_1$, $b_1$ は平方数 ($4,9,16,25,\dots$) で割れない自然数とかいて，$u = a_0a_1/b_0$ とおけば， \[ u^2r = a_1b_1 \] であり，$a_1$ と $b_1$ の公約数は $1$ だけであるから，$u^2r$ は平方数で割れない自然数である．すなわち，合同数は適切な正の有理数の平方をかけることによって，平方数で割れないような自然数の合同数になる．以下，平方数で割れないような自然数の合同数のことを，単に合同数と呼ぶことにする．$r$, $s$ にいろいろな値を入れてもなかなか $n$ が現れない場合に，$n$ が合同数でないのか，それとももっと別の $r$, $s$ の値を入れれば現れるのか，どちらかわからない．したがって，与えられた自然数 $n$ が合同数かどうかは簡単にはわからない．すでに見たように，$5$, $6$, $7$ は合同数である．$1$ は合同数でないことはフェルマーによって証明された．「与えられた自然数 $n$ が合同数かどうかを簡単に決定する方法を求める」を合同数問題 という．これは10世紀のアラビアに起源をさかのぼることができる古典的な問題であるが，現在でも完全には解決されていない．これは，楕円曲線

Tunnellの定理  $n$ を平方因数を持たないような奇数とする． 次の2つの条件を考える．

1. $n$ は合同数である．
2. $2x^2+y^2+8z^2=n$ を満たす整数 $x$, $y$, $z$ の組の個数は， $2x^2+y^2+32z^2=n$ を満たす整数 $x$, $y$, $z$ の組の個数の$2$倍に等しい．

そのとき，A ならば B が成り立つ．さらに，楕円曲線 $y^2=x^3-n^2x$ に対して Birch Swinerton-Dyer 予想が正しければ，B ならば A が成り立つ．

もう少し詳しく知りたい方は， (takadaH16.pdf) をご覧ください．

数学の研究について

高木貞治 著「近世数学史談」の中で述べられている，数学の研究についての一節を紹介します．

ガウスが進んだ道は即ち数学の進む道である．その道は帰納的である。特殊から一般へ！それが標語である。それは凡ての実質的なる学問に於て必要なる条件であらねばならない。数学が演繹的であるというが、それは既成数学の修業にのみ通用するのである。自然科学に於ても一つの学説が出来てしまえば、その学説に基づいて演繹をする。しかし論理は当り前なのだから、演繹のみから新しい物は何もでてこないのが当たり前であろう。若しも学問が演繹のみにたよるならば、その学問は小さな環の上を永遠に周期的に廻転する外はないであろう。我々は空虚なる一般論に捉われないで、帰納の一途に精進すべきではあるまいか。高木貞治「近世数学史談」P.57より