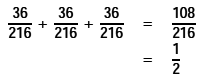取組実績と課題
5.「ここに注目!」数学の授業構成Q&A
・数学的内容の観点から
Q. どのようにしてこのサイコロの問題を見出されたのですか?
| A. | しばしば、確率論は賭博から生まれたといわれますが、この問題は、フランスのシュバリエ・ド・メレの有名な賭博の問題を参考にしました。メレの友人のバスカルは、彼から問題を提起されそれを数学的に分析し1つの合理的な回答を導き出しています。これが数学的確率の起源だと言われています。確率論の歴史の中には興味深い問題が数多くあります。確率論の歴史は、何らかの確率的事象によってわれわれ人類が直面する葛藤(自然に予想される結果と実際の結果との間の矛盾) とそれを克服しようとする努力の歴史でもあります。われわれはこのような問題を解決する過程で確率の考え方を発展させてきたといってもよいでしょう。したがって、確率論の歴史は、生徒が確率の考え方をその必要性・重要性とともに理解する助けとなりますし、「歴史的に生じた障害を分析することは生徒の数学の学習における困難を理解する助けともなります。」 数学史以外にも,意外性のある題材は教科書は問題集,数学教育関係の雑誌等にもあると思います。問題を選ぶ基準として,最も大切なことは,自分でその問題を解いてみて,あるいは,実際に実験をしてみて,「面白い」と思えるかどうかだと思います。 |
Q. この問題において、その葛藤とは何でしょうか?
| A. | ド・メレは、1個のサイコロを4回振って、1回でも6の目が出ることに賭けるときは、勝つ確率が高いということをおそらくは経験的に知っていたと思われます。2個のサイコロを投げてどちらも6の目が出る場合というのは、6×6=36通りのうちの1つであると考えた。そして、サイコロ1つの場合、6を出すのに4回で勝てるなら、サイコロ2つの場合は、その6倍すなわち、4×6=24の24回で勝てると考えた。つまり、彼の知っている唯一の数学である比例を適用して24回を導き出したのだが、メレはこの賭けに負けてしまうのである。数学的に正しいと確信しているのに、賭けの結果はその逆を示しているところにメレの葛藤が表れていると思います。 |
Q. この授業における葛藤の場面とはどこなのでしょう?
| A. | この葛藤の場面を如何に創りだすかが授業を構成する上での1つの重要な鍵となります。このサイコロの授業では、主に2つの場面があったと思います。まず1つ目の場面は、1時間目の授業、2つ目の場面は3時間目の授業にあります。 葛藤場面:確率は
<授業場面の描写>
ここで新たにつくり上げられた さて、この「比例的確率モデル」ですが、これは、1回投げて1の目が出る確率は6分の1だから、2回投げたらその確率は倍の6分の2、もし、6回投げたら確率もその6倍だから6分の6でほぼ確実に1の目が出るという比例に基づく考えを指しています。 |
Q. もっと具体的に教えてください。
| A. | 例えば、1時間目の開始から実験までのところでは、この「比例的確率モデル」を表出させる工夫がなされています。それは、[1]生徒が既にもっている素朴な確率の意味を慎重に見極めながら引き出すこと、[2]このアイディアに基づきながら、サイコロを振る回数を2回、6回、3回という順序で変化させながら問いかけている点です。回数を変化させることで比例の考えを想起させると同時に、この順序が心理的に重要であったと思っています。 |
Q. 「同様に確からしい」ということにふれられていませんが、何か意図はあったのでしょうか?
| A. | これは数学的確率の定義にかかわる重要なことがらです。一方、この授業のこの最初の3時間においては、同様に確からしいということが「明示的に」取り上げられることはありませんでした。暗黙的であったと思います。明示的に取り上げられるのは、赤-青カード問題の授業においてです。ここには、「起こり方」としての根元事象の重みづけが異なる場合がでてきます。そして、この問題を解決するためには、重みづけが同じということが必要になってきます。そのような必要に迫られた時に、重みづけが意識された時に「重みづけが同じ」ということを「同様に確からしい」というのですよと導入しています。 これは数学的な定義が出来上がったものとして最初にあるのではなく、発展的に修正されて最後に定式化されたものであるという考え方,数学本来の考え方を指導することを意図しているのです。 |
・数学の授業を支える指導技術的側面
| Q. | この実験は、1回の実験が「サイコロを3回振ること」で、この実験を10回するように生徒に指示すると、「サイコロを1回振ること」と「1回実験を行うこと」がごちゃ混ぜになってしまうが、どのような工夫がなされていたのですか? |
| A. | [1]「ちゃんと3回やって1セット」ということを言葉で投げかけること、[2] 1回の実験を教師が実演しながら、また生徒も実際に行うことを通して例示している。さらに、[3]生徒がこの実験過程と結果を記録するためのワークシート(指導案参照)を準備している。特に、[1]を忘れることはないが、[2]や[3]も指導方法の選択肢の1つとして心得ておくことが大切です。 また、「1回の実験が「サイコロを3回振ること」がいわゆる試行(trial)であり、その結果が事象(event)です。そして、もうこれ以上分けることが出来ない事象を根元事象(elementary event)といいます。そして、1つの試行で、根元事象の全体からなる事象 を、その試行の全事象(whole event)あるいは標本空間(sample space)といい、全事象に属する根元事象のどれが起こることも同じ程度に期待されるとき、これらの根元事象は同様に確からしい(equally likely, equi probable)という。 このように、1回の実験が「サイコロを3回振ること」であることを明確にすることは、確率論の考えで分析的に思考していくための出発点であり、非常に重要であることが分かります。この授業では、事象を「起こり方」と表現したり、その根元事象を(1,2,3) と表記し、樹形図の結果を表現したり、これらをベン図で表現された標本空間の要素として表現するなど、意図的・計画的に発展的に用いられています。授業ビデををみる時の1つのポイントになると思います。 |
| Q. | この授業では、先生の板書がとても印象的で分かりやすく思ったのですが、何かポイントとなるところはあるのでしょうか? |
| A. | 確かに、比較的きれいに板書されていたので、印象的だったと思います。まず、授業中に生徒に投げかける重要な発問や課題、さらには、生徒から出された考えなどは、口頭だけでなく板書しておくと、残るので、後の議論の対象にすることができます。一方、樹形図などの考え方を全部書かないこと、書きすぎないことも重要です。中学校では、時間がないから、生徒に考えさせるべきことまで書いてしまうことがあります。例示的なところでとめることも大切だと思います。例えば、樹形図などは、はじめてかくことだから、全く何もない状態で書くっていうのは無理があります。適宜例示的に書くことで、生徒は、こうやって書いていくと出せそうだなっていう安心がもてて、でも考えるところも残して・・・というようにするとよいと思います。 |
| Q. | この授業では、先生が何度も同じようなことを繰り返し生徒に聞いているようにみえるのですが・・・それは大切なことなのでしょうか? |
| A. | この授業では、先生が何度も同じようなことを繰り返し生徒に聞いているようにみえるのですが・・・それは大切なことなのでしょうか? |
Q. それはどうして大切なことなのでしょうか?
| A. | 例えば、216通りの「起こり方」についてある女子生徒が説明している場面がありました。これは確率の分母に当たる数値です。分母にあたる部分を本当に理解していないと確率そのものの理解につながりません。とかく教師は「待ってました」という答えをある生徒が言ってくれるとほっとします、あとは大丈夫かなと思いたくなります。ところが、必ずしも発言していない生徒が分かっているかというとそうではなく、分かっていない生徒が多いのです。この授業の中で、この問題については、216の出し方を本当にわかったかというのは、この授業もそうですし、この後の指導にも大事になるのです。 おそらく授業者から見ると、あの生徒がわかってれば、他の生徒も本当に分かったんだろうなという生徒に指名してるんだろうなという気がします。だから、もう一人、教師からみて数学的に不安かなという生徒を指名して、確かにその子も言える。なら次に行こうという。二人目の生徒が一つの、授業としてのハードルを越えたかということを、その授業の中で評価しているんです。だから、大事にしたいなと思います。 |
| Q. | この授業の3時間目に生徒に問題作りをさせている場面がとても面白いと思いました。これにはどんな意図があったのでしょうか? |
| A. | そうですね、複雑な樹形図が完成した後、この樹形図を使って、1つのサイコロを3回振るという同じ場面設定でいろんな問題を生徒が考えている場面ですね。この意図は、1つには、この場面設定はこの樹形図という1つの数学的モデルによってある程度支配 できるということを実感として理解してほしかった、樹形図の威力というかパワー、よさですね、これを理解する機会となるということが1つ。もう一つは、問題を作らせるとこの過程を通して生徒の理解の状態が教師側に見えます。問題作りは子どもたちの理 解をみるための窓のような役割もあります。子どもたちの主体的な活動が実現されるのもとてもよいと思います。 |